Mathematics
The adjoining sketch shows a running track 3.5 m wide all around which consists of two straight paths and two semicircular rings. Find the area of the track.
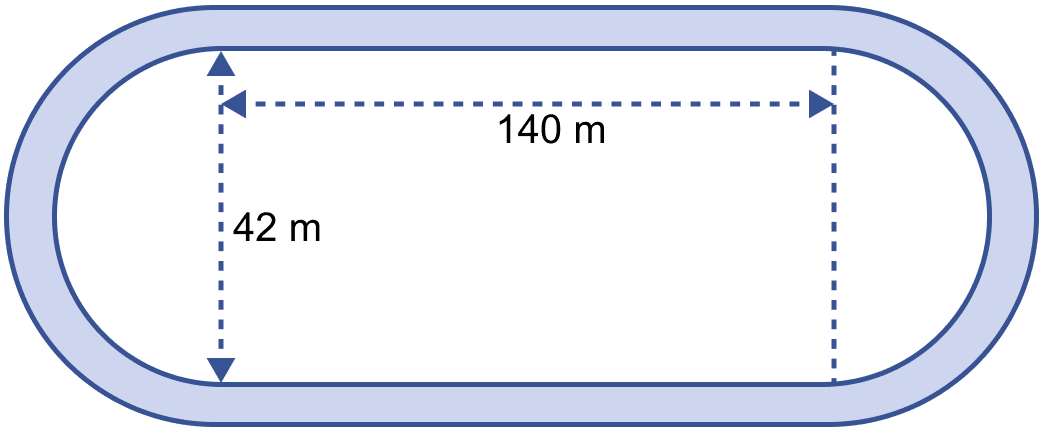
Mensuration
5 Likes
Answer
From figure,
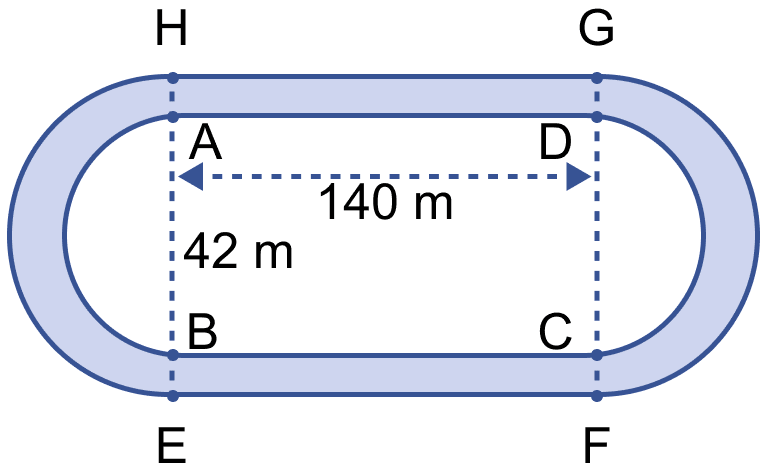
Length of inner rectangle ABCD = 140 m
Breadth of inner rectangle ABCD = 42 m
Diameter of inner semi-circle = 42 m
Radius of inner semi-circle (r) = = 21 m.
Length of outer rectangle = Length of inner rectangle = 140 m
Breadth of outer rectangle = Breadth of inner rectangle + 2 × Width of outer track = 42 + 2 × 3.5 = 42 + 7 = 49 m.
Diameter of outer semi-circle = 49 m
Radius of outer semi-circle (R) = = 24.5 m.
Area of track = Area of outer rectangle - Area of inner rectangle + 2(Area of outer semi-circle - Area of inner semi-circle)
Hence, area of track = 1480.5 m2.
Answered By
2 Likes
Related Questions
If the diameter of a semi-circular protractor is 14 cm, then find its perimeter.
A road 3.5 m wide surrounds a circular park whose circumference is 88 m. Find the cost of paving the road at the rate of ₹60 per square metre.
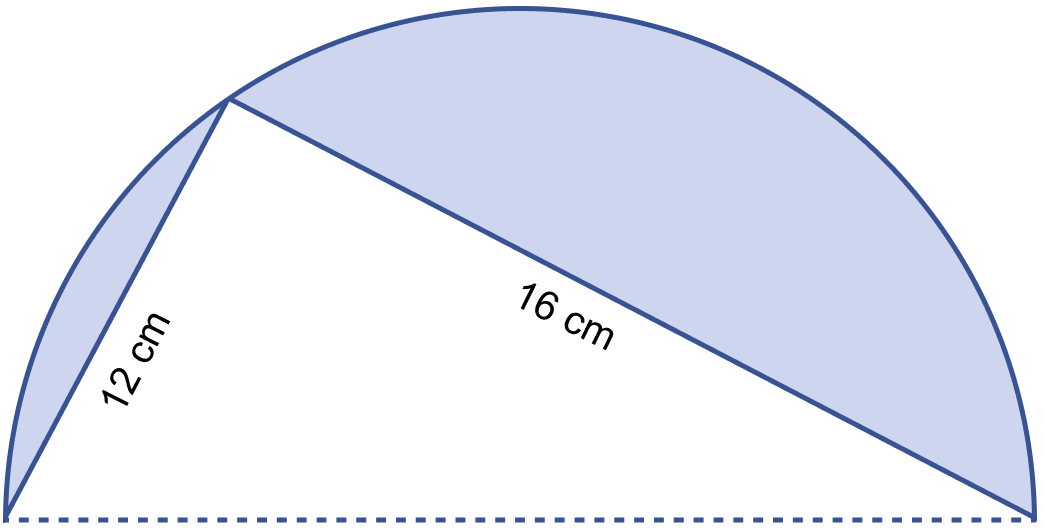
In the adjoining figure, O is the center of a circular arc and AOB is a line segment. Find the perimeter and the area of the shaded region correct to one decimal place. (Take π = 3.142)
In the figure (i) given below, the radius is 3.5 cm. Find the perimeter of the quarter of the circle.
