Mathematics
Solve the following system of linear equations graphically :
2x - y - 4 = 0, x + y + 1 = 0.
Hence, find the area of the triangle formed by these lines and the y-axis.
Coordinate Geometry
30 Likes
Answer
Given,
⇒ 2x - y - 4 = 0
⇒ y = 2x - 4 …………(1)
When x = 1, y = 2(1) - 4 = 2 - 4 = -2,
x = 2, y = 2(2) - 4 = 4 - 4 = 0,
x = 3, y = 2(3) - 4 = 6 - 4 = 2.
Table of values for equation (1)
| x | 1 | 2 | 3 |
|---|---|---|---|
| y | -2 | 0 | 2 |
Steps of construction :
Plot the points (1, -2), (2, 0) and (3, 2).
Join the points.
Given,
⇒ x + y + 1 = 0
⇒ y = -(x + 1) ………….(2)
When, x = -1, y = -(-1 + 1) = 0,
x = 0, y = -(0 + 1) = -1,
x = 1, y = -(1 + 1) = -2.
Table of values for equation (2)
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 0 | -1 | -2 |
Steps of construction :
Plot the points (-1, 0), (0, -1) and (1, -2).
Join the points.
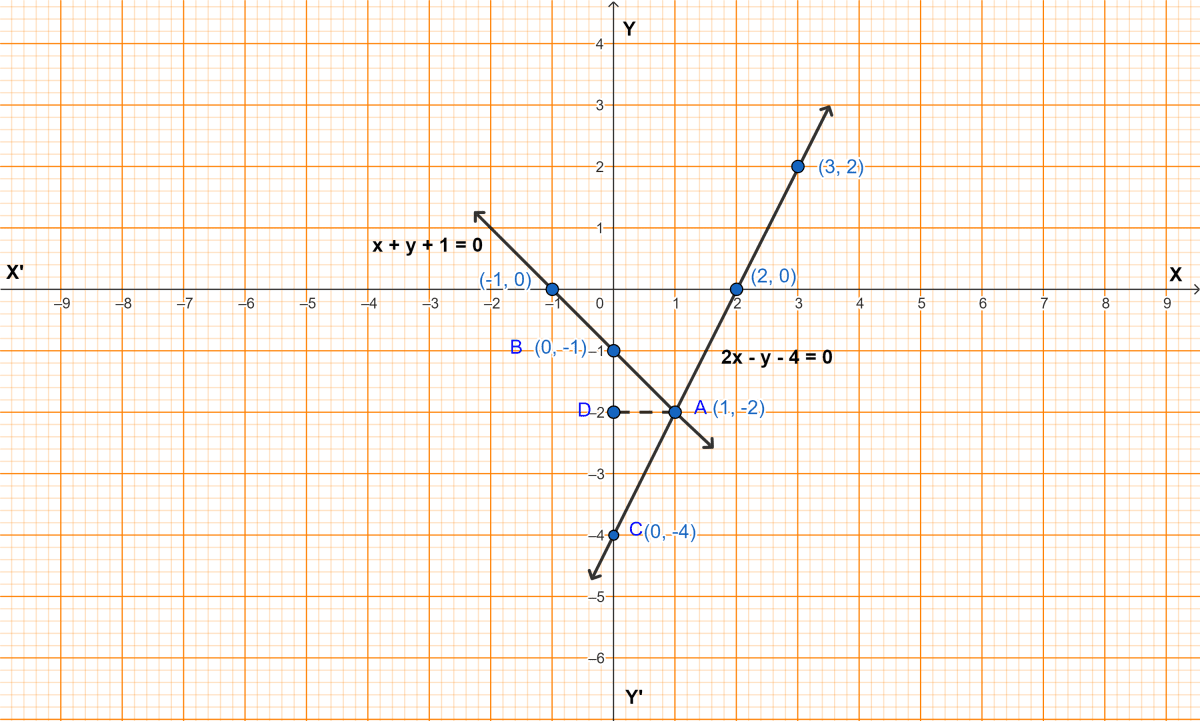
From graph,
A(1, -2) is the point of intersection of lines.
ABC are the vertices of triangle.
From A, draw AD perpendicular to BC.
AD = 1 unit and BC = 3 units.
Area of △ABC = × base × height
= × BC × AD
= × 3 × 1
= sq. units
Hence, point of intersection = (1, -2) and area of triangle = sq. units
Answered By
11 Likes
Related Questions
Solve the following simultaneous equations, graphically :
2x - 3y + 2 = 4x + 1 = 3x - y + 2.
Use graph paper for this question :
(i) Draw the graphs of 3x - y - 2 = 0 and 2x + y - 8 = 0. Take 1 cm = 1 unit on both axes and plot three points per line.
(ii) Write down the coordinates of the point of intersection and the area of the triangle formed by the lines and the x-axis.
Solve graphically the following equations :
x + 2y = 4, 3x - 2y = 4.
Take 2 cm = 1 unit on each axis. Write down the area of the triangle formed by the lines and the x-axis.
On graph paper, take 2 cm to represent one unit on both axes, draw the lines :
x + 3 = 0, y - 2 = 0, 2x + 3y = 12.
Write down the coordinates of the vertices of the triangle formed by these lines.