Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

Since, diagonals bisect each other at 90°

∴ ∠AOB = ∠COD = BOC = AOD = 90°.

From figure,

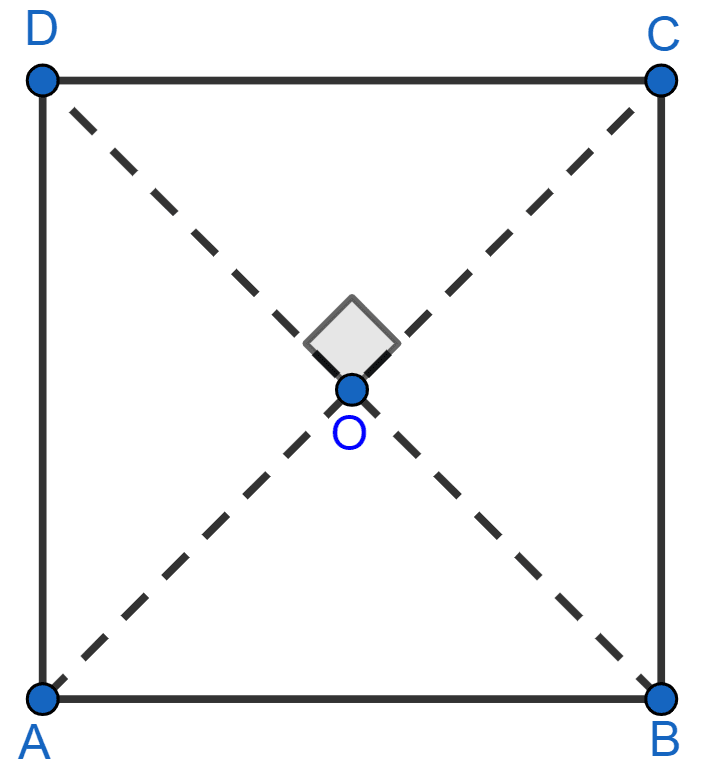
Considering △OAB and △ODC we have,

⇒ OA = OC (As diagonals bisect each other)

⇒ OB = OD (As diagonals bisect each other)

⇒ ∠AOB = ∠COD (Vertically opposite angles are equal)

Hence, △OAB ≅ △ODC by SAS axiom.

AB = CD (By C.P.C.T.) ………(i)

∴ ∠OAB = ∠OCD (By C.P.C.T.)

The above angles are alternate angles.

Hence, we can say that AB || CD.

In △AOB,

OA = OB (As both diagonals are equal and bisect each other)

so,

⇒ ∠OBA = ∠OAB = x (let) (Angles opposite to equal sides are equal in isosceles triangle)

⇒ ∠OBA + ∠OAB + ∠AOB = 180°

⇒ x + x + 90° = 180°

⇒ 2x = 180° - 90°

⇒ 2x = 90°

⇒ x = $\dfrac{90°}{2}$

⇒ x = 45°.

Considering △OAD and △OBC we have,

⇒ OA = OC (As diagonals bisect each other)

⇒ OB = OD (As diagonals bisect each other)

⇒ ∠AOD = ∠COB (Vertically opposite angles are equal)

Hence, △OAD ≅ △OBC by SAS axiom.

AD = BC (By C.P.C.T.) ………(ii)

∠OAD = ∠OCB (By C.P.C.T.)

Hence, we can say that AD || BC.

Considering △AOB and △AOD we have,

⇒ AO = AO (Common side)

⇒ OB = OD (As diagonals bisect each other)

⇒ ∠AOD = ∠AOB (Both equal to 90°)

Hence, △AOB ≅ △AOD by SAS axiom.

AB = AD (By C.P.C.T.) ………(iii)

From (i), (ii) and (iii) we get,

AB = BC = CD = AD.

In △AOD,

OA = OD (As both diagonals are equal and bisect each other)

so,

⇒ ∠OAD = ∠ODA = a (let) (Angles opposite to equal side are equal in isosceles triangle)

⇒ ∠OAD + ∠ODA + ∠AOD = 180°

⇒ a + a + 90° = 180°

⇒ 2a = 180° - 90°

⇒ 2a = 90°

⇒ a = $\dfrac{90°}{2}$

⇒ a = 45°.

∠A = ∠OAB + ∠OAD = 45° + 45° = 90°.

Thus, AB ⊥ AD.

Since, AD || BC so, AB ⊥ BC.

Since, AB || CD and AB ⊥ AD,

∴ CD ⊥ AD.

Since, alternate sides are perpendicular and all sides are equal.

Hence, proved that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square