Mathematics
Represent each of the following on different number lines :
.
Rational Irrational Nos
23 Likes
Answer
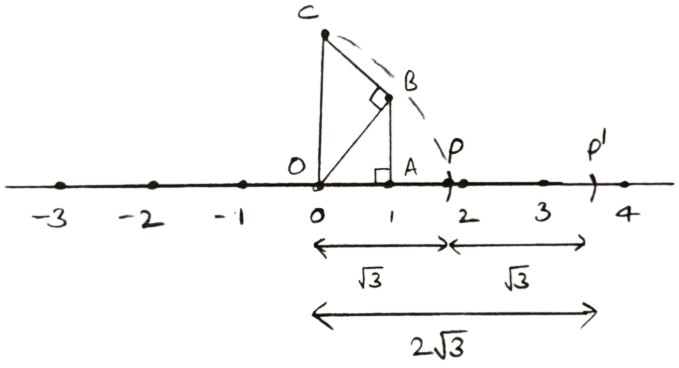
Steps of construction of :
- Take OA = AB = 1 unit and ∠OAB = 90°, so by pythagoras theorem :
⇒ OB2 = OA2 + AB2
⇒ OB2 = 12 + 12
⇒ OB2 = 1 + 1
⇒ OB2 = 2
⇒ OB = unit - Draw BC = AB = OA = 1 unit and ∠OBC = 90°.
- By pythagoras theorem :
⇒ OC2 = OB2 + BC2
⇒ OC2 =
⇒ OC2 = 2 + 1
⇒ OC2 = 3
⇒ OC = unit. - With point O as center and OC as radius darw an arc which meets the number line at point P.
OP = OC = . - With P as center and OP as radius draw an arc cutting number line at P', so PP' =
OP' = OP + PP' = .
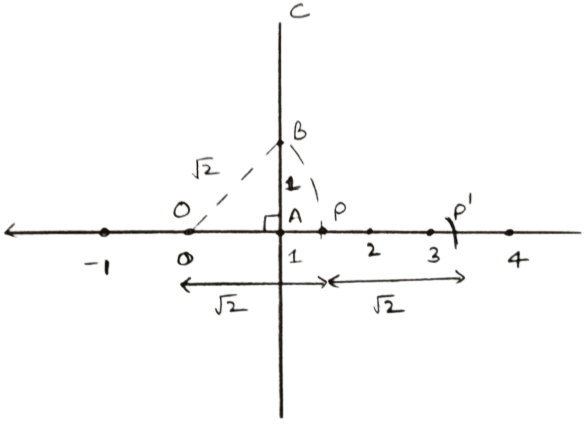
Steps of construction of :
- Mark O of the number line at point 0.
- On the same number line, mark 1 as point A i.e., take OA = 1 unit
- At point A, draw AC perpendicular to the number line.
- From AC, cut AB = 1 unit = OA, then join A and B.
Using pythagoras theorem, we get :
OB2 = OA2 + AB2
OB2 = 12 + 12
OB2 = 1 + 1 = 2
OB = . - Taking point O as center and OB = as radius, draw an arc which cuts the number line at point P.
Clearly, OP = OB = - With P as center and OP as radius draw an arc intersecting number line at P'.
OP' = OP + PP' = .
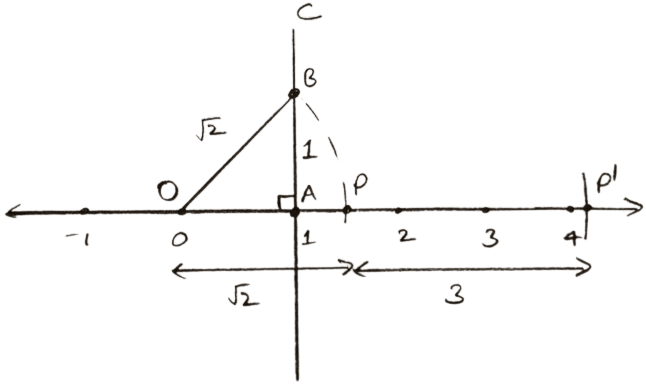
Steps of construction of
- Mark O of the number line at point 0.
- On the same number line, mark 1 as point A i.e., take OA = 1 unit
- At point A, draw AC perpendicular to the number line.
- From AC, cut AB = 1 unit = OA, then join O and B.
Using pythagoras theorem, we get :
OB2 = OA2 + AB2
OB2 = 12 + 12
OB2 = 1 + 1 = 2
OB = . - Taking point O as center and OB = as radius, draw an arc which cuts the number line at point P.
Clearly, OP = OB = - From point P as center and radius = 3 cm draw an arc intersecting number line at P'.
OP' = OP + PP' = .
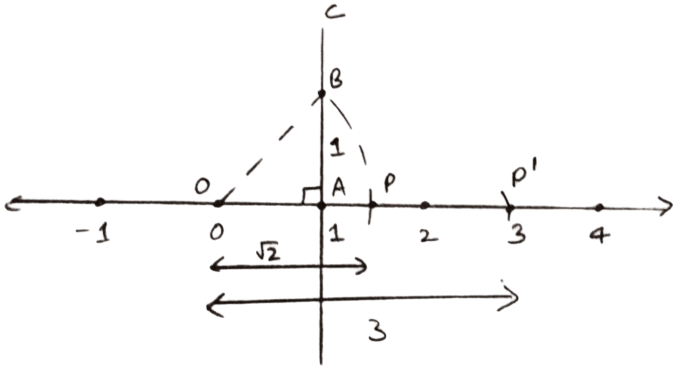
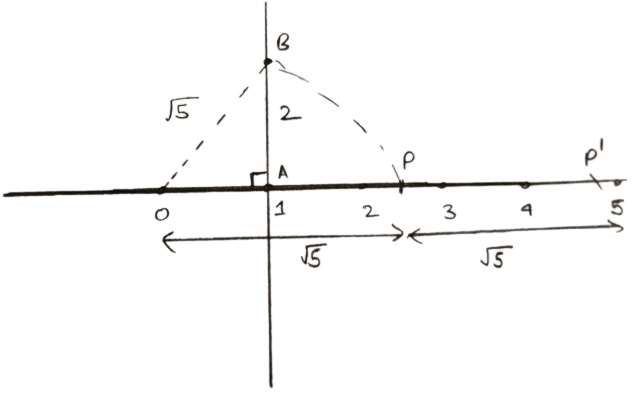
Steps of construction of
- Mark O of the number line at point 0.
- On the same number line, mark 1 as point A i.e., take OA = 1 unit
- At point A, draw AC perpendicular to the number line.
- From AC, cut AB = 1 unit = OA, then join O and B.
Using pythagoras theorem, we get :
OB2 = OA2 + AB2
OB2 = 12 + 12
OB2 = 1 + 1 = 2
OB = . - Taking point O as center and OB = as radius, draw an arc which cuts the number line at point P.
Clearly, OP = OB = - From point O as center and radius = 3 unit draw an arc intersecting number line at P'.
PP' = OP' - OP = .
Steps of construction of :
- Mark O of the number line at point 0.
- On the same number line, mark 1 as point A i.e., take OA = 1 unit
- At point A, draw AC perpendicular to the number line.
- From AC, cut AB = 2 unit, then join O and B.
Using pythagoras theorem, we get :
OB2 = OA2 + AB2
OB2 = 12 + 22
OB2 = 1 + 4 = 5
OB = . - Taking point O as center and OB = as radius, draw an arc which cuts the number line at point P.
Clearly, OP = OB = - From point P as center and OP as radius draw an arc intersecting number line at P'.
OP' = OP + PP' = .
Answered By
9 Likes