Mathematics
PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate :
(i) ∠CBT
(ii) ∠BAT
(iii) ∠APT
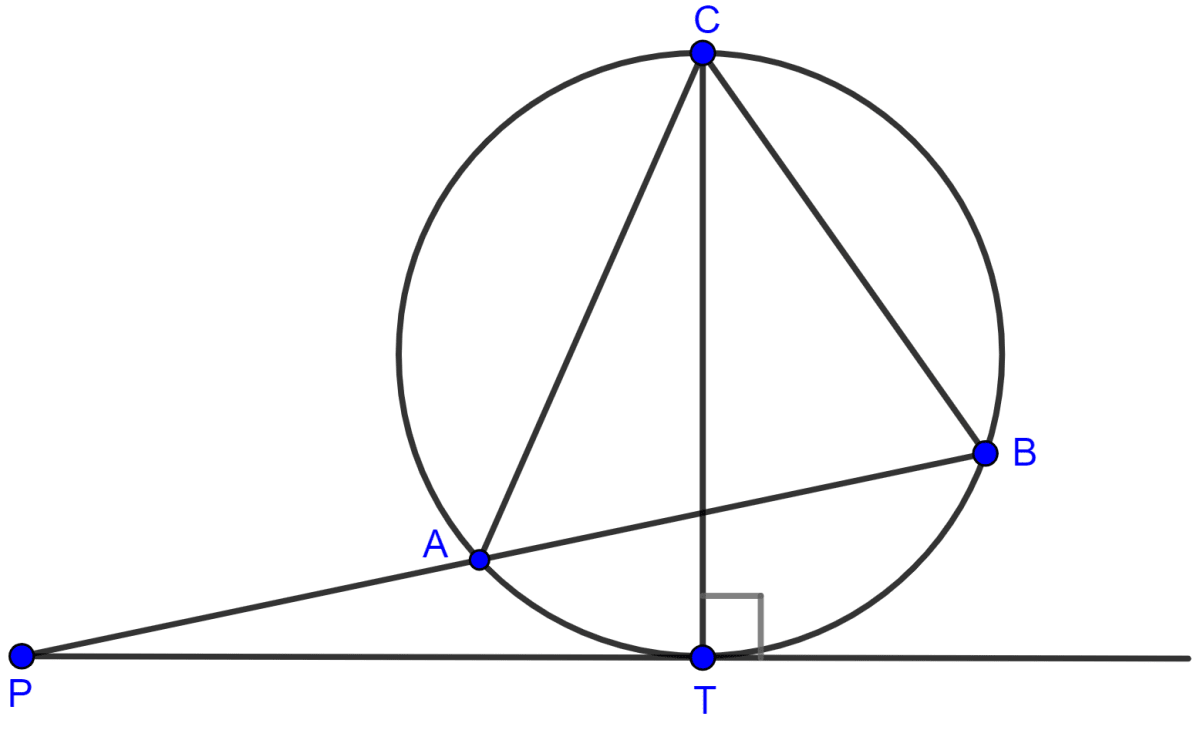
Circles
24 Likes
Answer
Join AT and BT.
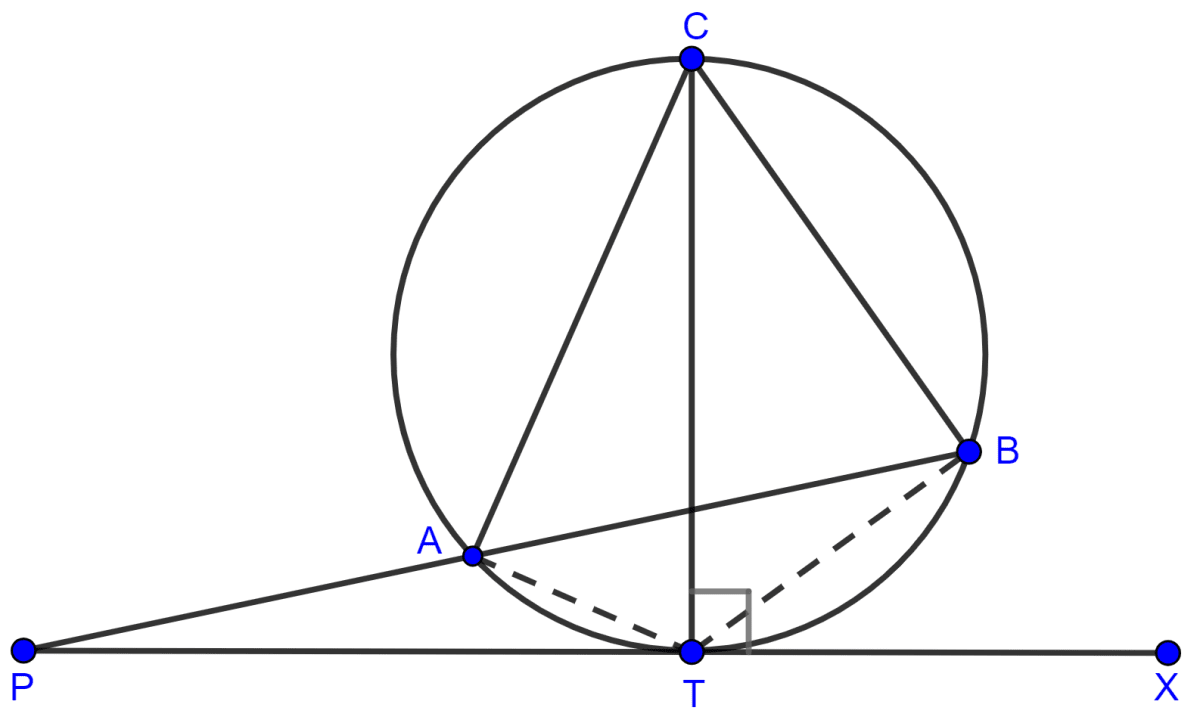
(i) TC is the diameter of the circle.
Since, angle in a semi-circle is a right angle.
∴ ∠CBT = 90°.
Hence, ∠CBT = 90°.
(ii) In cyclic quadrilateral ATBC,
⇒ ∠CBT + ∠CAT = 180° (∵ Sum of opposite angles of a cyclic quadrilateral = 180°)
⇒ 90° + ∠CAT = 180°
⇒ ∠CAT = 180° - 90°
⇒ ∠CAT = 90°.
In △ABC,
⇒ ∠CBA + ∠CAB + ∠ACB = 180° [By angle sum property of triangle]
⇒ 70° + ∠CAB + 50° = 180°
⇒ ∠CAB + 120° = 180°
⇒ ∠CAB = 180° - 120°
⇒ ∠CAB = 60°.
From figure,
∠BAT = ∠CAT - ∠CAB = 90° - 60° = 30°.
Hence, ∠BAT = 30°.
(iii) From figure,
∠BTX = ∠BAT = 30° [Angle in same segment are equal]
∠PBT = ∠CBT - ∠CBA = 90° - 70° = 20°.
⇒ ∠PTB = 180° - ∠BTX = 180° - 30° = 150°.
In △PBT,
⇒ ∠PBT + ∠PTB + ∠APT = 180° [By angle sum property of triangle]
⇒ 20° + 150° + ∠APT = 180°
⇒ ∠APT + 170° = 180°
⇒ ∠APT = 180° - 170°
⇒ ∠APT = 10°.
Hence, ∠APT = 10°.
Answered By
14 Likes
Related Questions
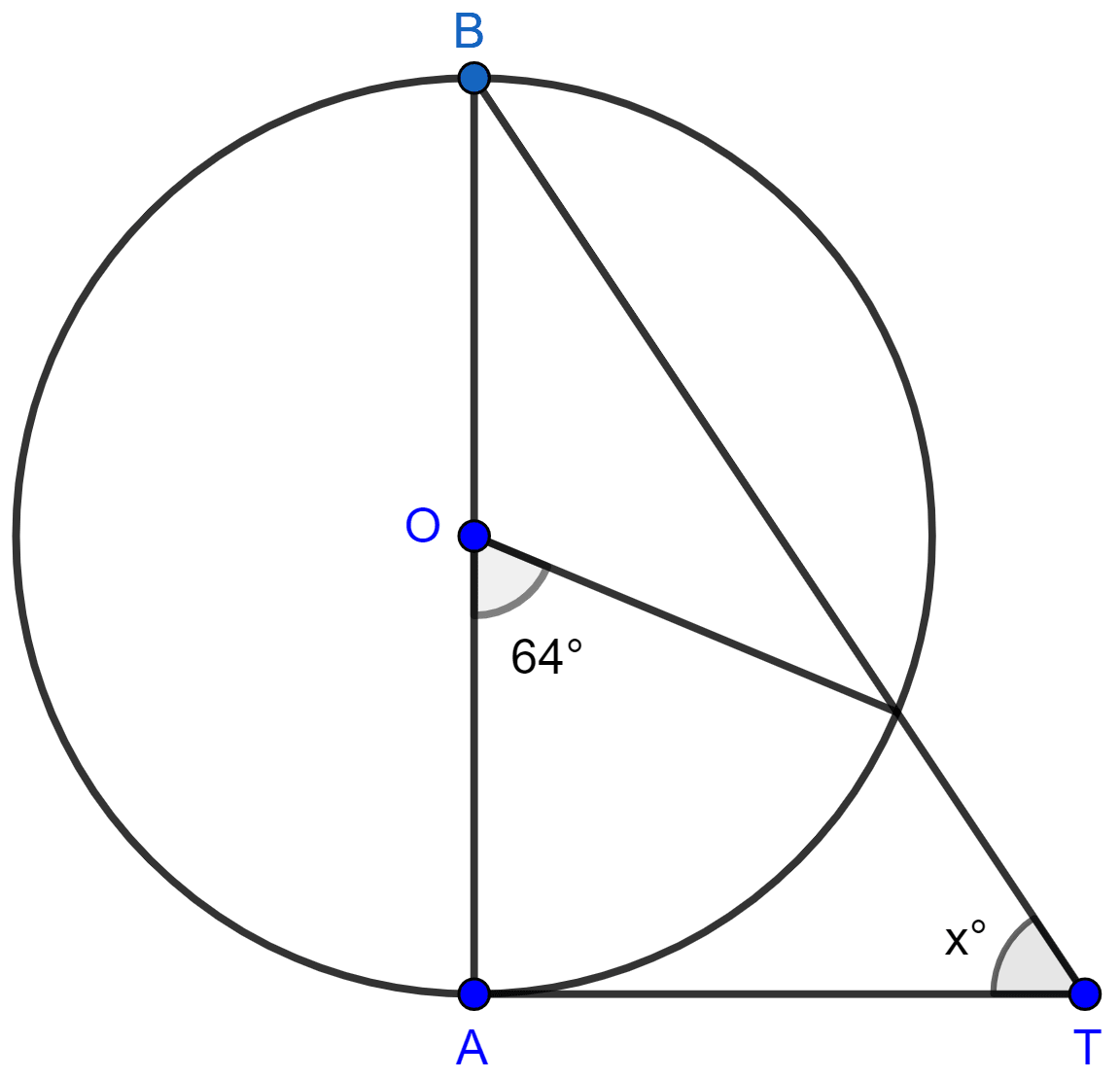
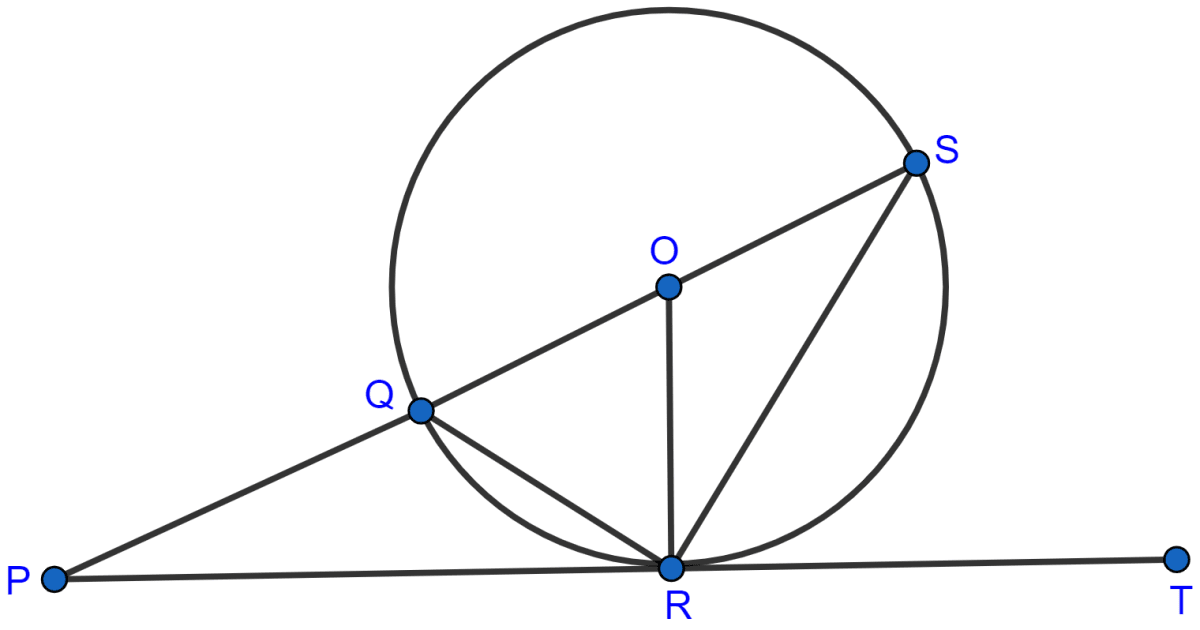
In the given figure, PT touches the circle with center O at point R. Diameter SQ is produced to meet the tangent TR at P.
Given ∠SPR = x° and ∠QRP = y°;
prove that :
(i) ∠ORS = y°
(ii) write an expression connecting x and y.
In the given figure, O is the center of the circumcircle ABC. Tangents A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.
In the given figure, PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ = 30°, prove that : BD is diameter of the circle.
In the given figure, AB is the diameter of the circle, with center O, and AT is the tangent. Calculate the numerical value of x.
