KnowledgeBoat Logo

Mathematics

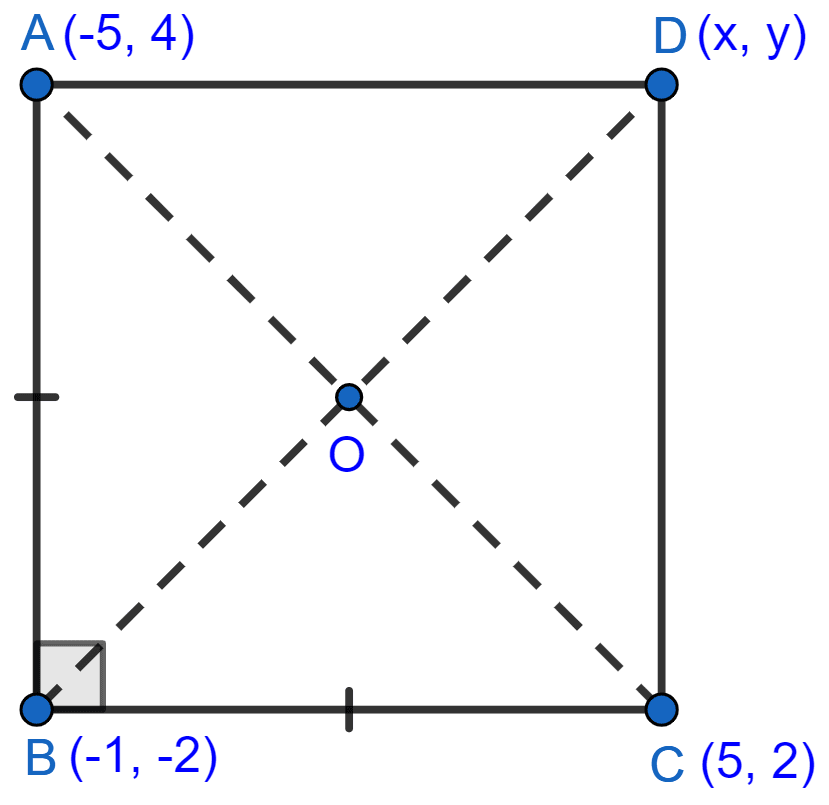
Prove that the points A(-5, 4); B(-1, -2) and C(5, 2) are the vertices of an isosceles right angled triangle. Find the co-ordinates of D so that ABCD is a square.

Section Formula

12 Likes

Answer

The points are shown in the figure below:

Prove that the points A(-5, 4); B(-1, -2) and C(5, 2) are the vertices of an isosceles right angled triangle. Find the co-ordinates of D so that ABCD is a square. Section and Mid-Point Formula, Concise Mathematics Solutions ICSE Class 10.

Distance between two points = (x2−x1)2+(y2−y1)2\sqrt{(x2 - x1)^2 + (y2 - y1)^2}

AB=[−1−(−5)]2+[−2−4]2=[−1+5]2+[−6]2=[4]2+36=16+36=52.BC=[5−(−1)]2+[2−(−2)]2=[5+1]2+[4]2=[6]2+16=36+16=52.AC=[5−(−5)]2+[2−4]2=[5+5]2+[−2]2=[10]2+4=100+4=104.AB2+BC2=(52)2+(52)2=52+52=104=AC2.AB = \sqrt{[-1 - (-5)]^2 + [-2 - 4]^2} \\[1em] = \sqrt{[-1 + 5]^2 + [-6]^2} \\[1em] = \sqrt{[4]^2 + 36} \\[1em] = \sqrt{16 + 36} \\[1em] = \sqrt{52}. \\[1em] BC = \sqrt{[5 - (-1)]^2 + [2 - (-2)]^2} \\[1em] = \sqrt{[5 + 1]^2 + [4]^2} \\[1em] = \sqrt{[6]^2 + 16} \\[1em] = \sqrt{36 + 16} \\[1em] = \sqrt{52}. \\[1em] AC = \sqrt{[5 - (-5)]^2 + [2 - 4]^2} \\[1em] = \sqrt{[5 + 5]^2 + [-2]^2} \\[1em] = \sqrt{[10]^2 + 4} \\[1em] = \sqrt{100 + 4} \\[1em] = \sqrt{104}. \\[1em] AB^2 + BC^2 = (\sqrt{52})^2 + (\sqrt{52})^2 \\[1em] = 52 + 52 \\[1em] = 104 = AC^2.

Since, AB = BC and AC2 = AB2 + BC2.

Hence, proved that ABC is an isosceles right angled triangle.

Since, diagonals of square bisect each other so,

Mid-point of AC = Mid-point of BD = O.

O=(−5+52,4+22)=(02,62)=(0,3).O = \Big(\dfrac{-5 + 5}{2}, \dfrac{4 + 2}{2}\Big) \\[1em] = \Big(\dfrac{0}{2}, \dfrac{6}{2}\Big) \\[1em] = (0, 3).

Let co-ordinates of D = (x, y).

∴O=(−1+x2,−2+y2)⇒(0,3)=(−1+x2,−2+y2)⇒0=−1+x2 and 3=−2+y2⇒−1+x=0 and −2+y=6⇒x=1 and y=8.\therefore O = \Big(\dfrac{-1 + x}{2}, \dfrac{-2 + y}{2}\Big) \\[1em] \Rightarrow (0, 3) = \Big(\dfrac{-1 + x}{2}, \dfrac{-2 + y}{2}\Big) \\[1em] \Rightarrow 0 = \dfrac{-1 + x}{2} \text{ and } 3 = \dfrac{-2 + y}{2} \\[1em] \Rightarrow -1 + x = 0 \text{ and } -2 + y = 6 \\[1em] \Rightarrow x = 1 \text{ and } y = 8.

D = (x, y) = (1, 8).

Hence, co-ordinates of D = (1, 8).

Answered By

5 Likes

Related Questions