Prove that the loss in weight of a body when immersed wholly or partially in a liquid is equal to the buoyant force (or upthrust) and this loss is because of the difference in pressure exerted by liquid on the upper and lower surfaces of the submerged part of the body.

Consider a cylindrical body PQRS of cross-sectional area A immersed in a liquid of density ρ as shown in the figure. Let the upper surface PQ of body be at a depth h₁ while it's lower surface RS be at a depth h₂ below the free surface of liquid.

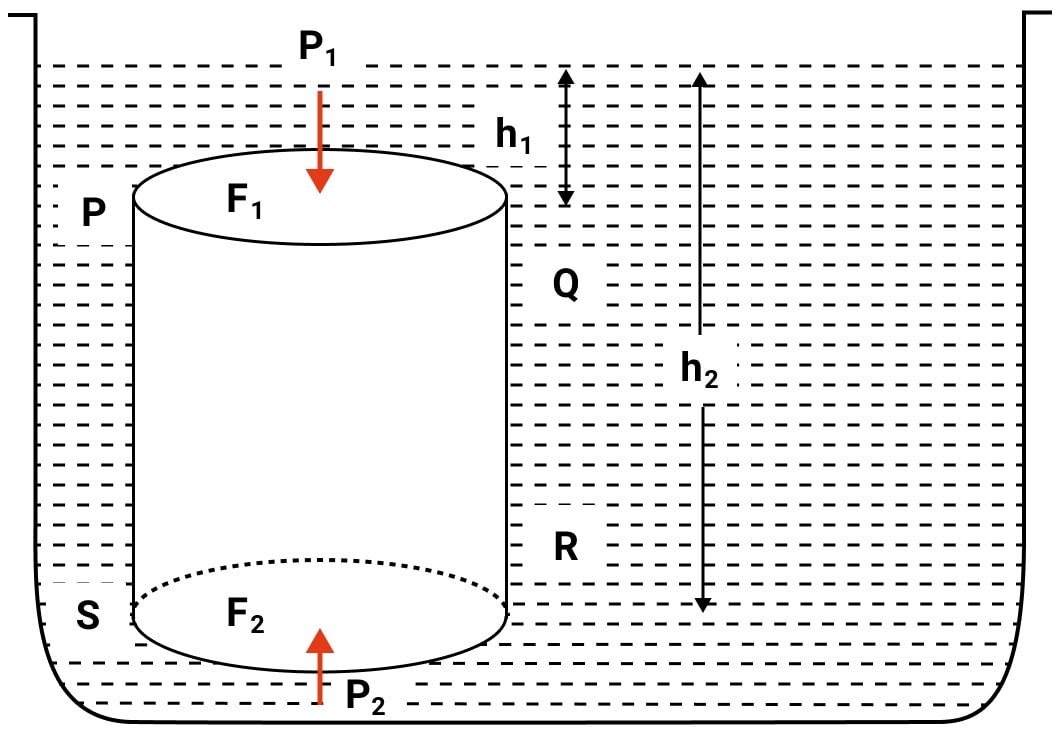
At depth h₁, the pressure on the upper surface PQ

P₁ = h₁ ρ g

∴ Downward thrust on the upper surface PQ

F₁ = pressure x area = h₁ ρ g A    [Equation 1]

At depth h₂, the pressure on the lower surface RS

P₂ = h₂ ρ g

∴ Upward thrust on the lower surface RS

F₂ = pressure x area = h₂ ρ g A    [Equation 2]

The horizontal thrust at various points on the vertical sides of the body get balanced because liquid pressure is same at all points at the same depth.

From above equations (1) and (2), it is clear that F₂ > F₁ as h₂ > h₁ and hence the body will experience a net upward force.

Resultant upward thrust on the body

F_B = F₂ – F₂

= h₂ρgA - h₂ρgA

= A(h₂ - h₁)ρg

But, A(h₂ - h₁) = V, the volume of the body submerged in the liquid.

∴ Upthrust F_B = Vρg

Vρg = Volume of solid immersed x density of liquid x acceleration due to gravity

Since a solid when immersed in a liquid, displaces liquid equal to the volume of its submerged part, therefore

Vρg = Volume of liquid displaced x density of liquid x acceleration due to gravity

= mass of liquid displaced x acceleration due to gravity

= weight of the liquid displaced by the submerged part of the body.

Hence,

Upthrust = weight of the liquid displaced by the submerged part of the body.

Now in another experiment, we suspend a solid by a thin thread attached to the hook of a spring balance to check its weight. Once the weight is noted, we fill a eureka can with water till its spout and place a measuring cylinder below the spout of the eureka can. The solid is then immersed in water and the displaced water is collected in the cylinder.

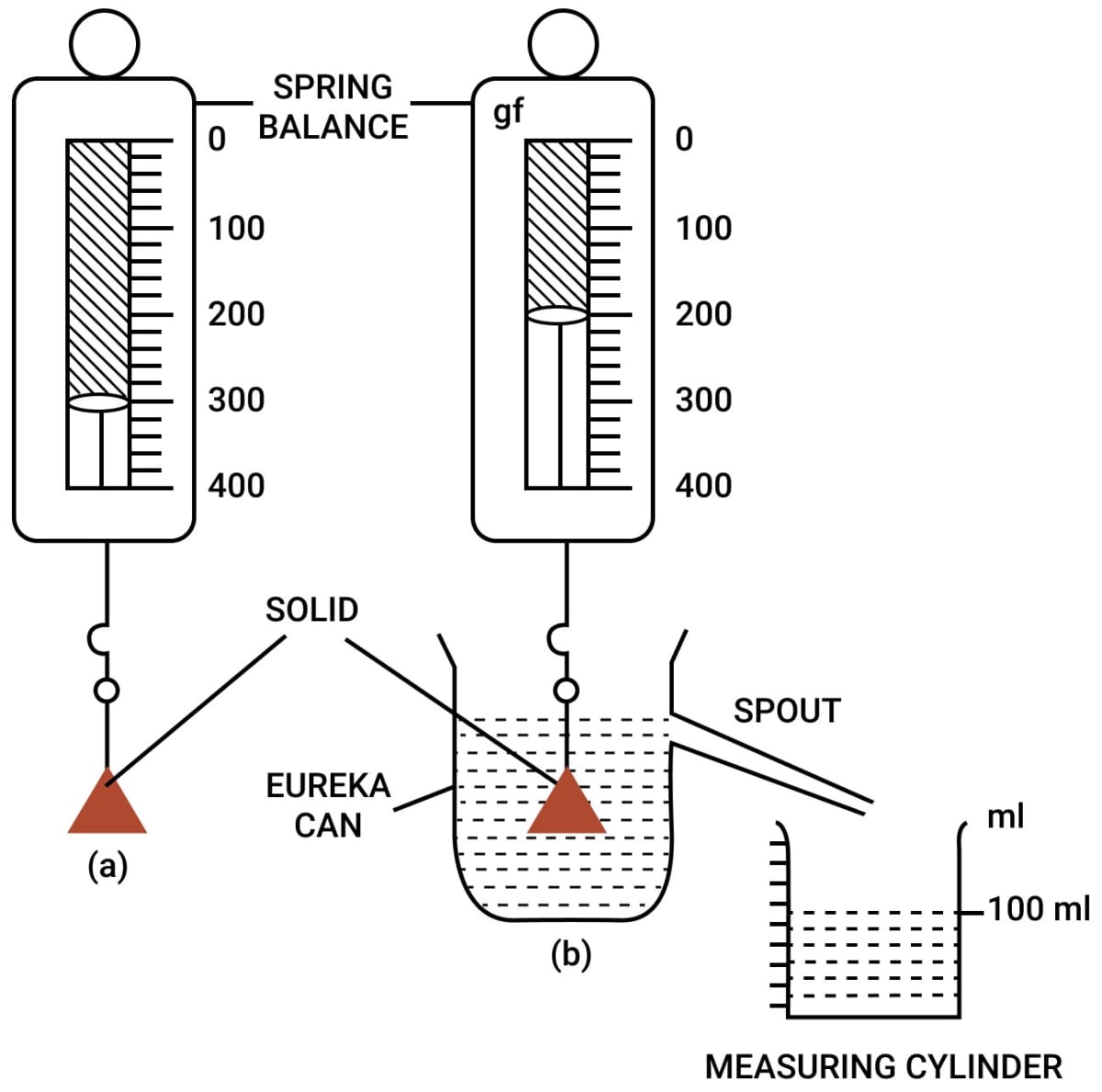
When the water stops dripping, the weight of the solid and the volume of water in the cylinder are noted.

In the above figure, the solid weighs 300 gf in air and 200 gf when it is completely immersed in water. The volume of water collected in the measuring cylinder is 100 ml i.e., 100 cm³

∴ Loss in weight = 300 gf - 200 gf = 100 gf   [Equation 1]

Volume of water displaced = Volume of solid = 100 cm³

∵ Density of water = 1 g cm^-3

∴ Weight of water displaced = 100 gf    [Equation 2]

From equations 1 and 2,

Weight of water displaced = Upthrust or loss in weight.

Thus, the weight of water displaced by a solid is equal to the loss in weight of solid.