Mathematics
One of the diagonals of a rhombus and its sides are equal. Find the angles of the rhombus.
Quadrilaterals
25 Likes
Answer
One of the diagonals of a rhombus and its sides are equal.
ABCD is the rhombus and AC is the diagonal such that AC = AB.
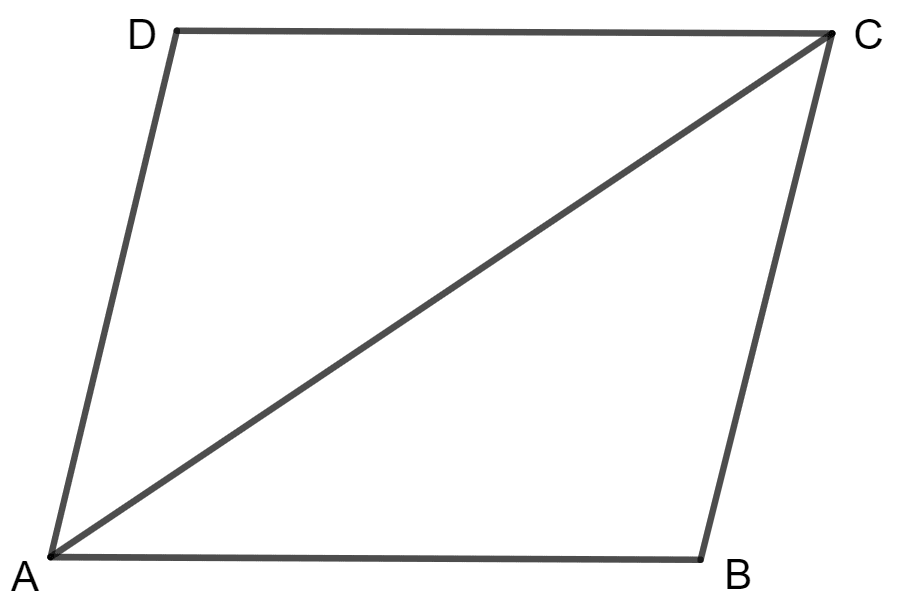
In triangle ABC,
AB = BC (Sides of rhombus)
AB = AC (Given)
⇒ AB = AC = BC
So, triangle ABC is a equilateral triangle.
Therefore, ∠ B = 60°, ∠ BAC = 60° and ∠ BCA = 60°.
Similarly, triangle ADC is a equilateral triangle.
Therefore, ∠ D = 60°, ∠ DAC = 60° and ∠ DCA = 60°
∠ A = ∠ BAC + ∠ DAC
= 60° + 60°
= 120°
∠ C = ∠ BCA + ∠ DCA
= 60° + 60°
= 120°
Hence, the value of ∠ A = 120°, ∠ B = 60°, ∠ C = 120° and ∠ D = 60°.
Answered By
17 Likes
Related Questions
In the given figure, ABCD is a parallelogram. If OA = 6 cm and AC - BD = 2 cm; find the length of BD.
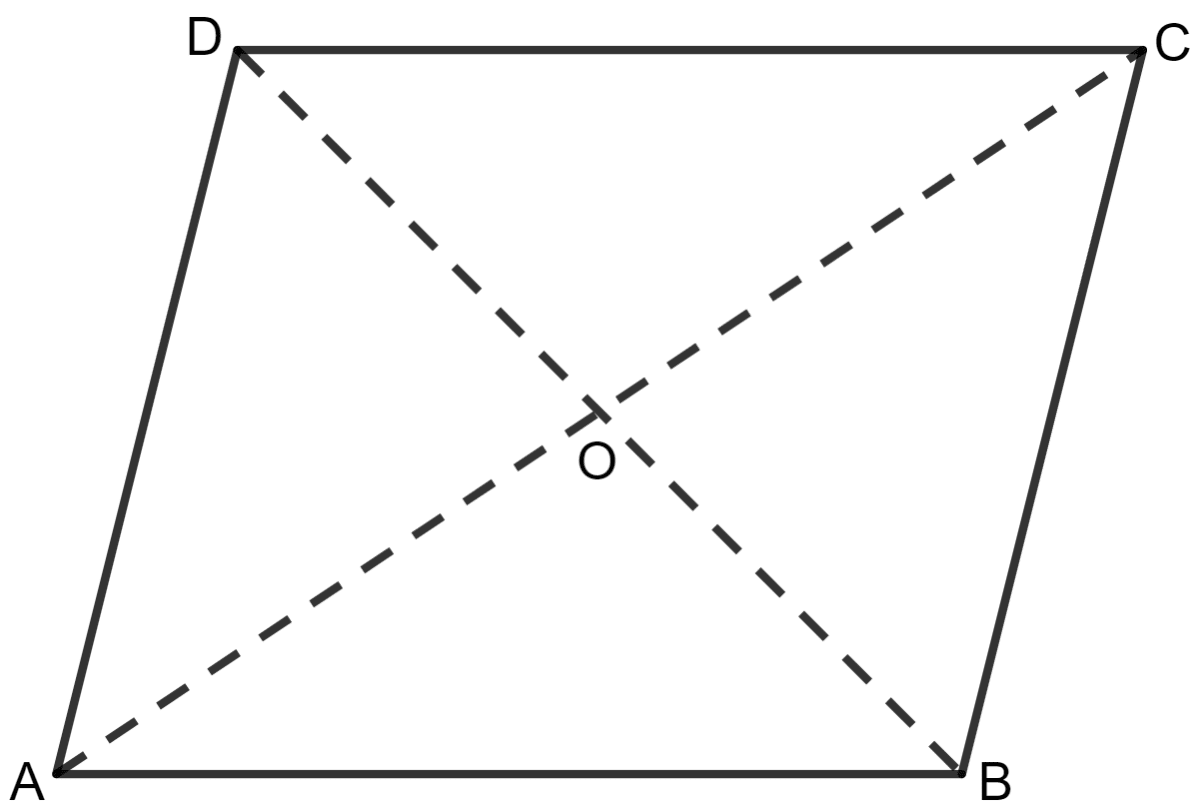
The diagonals of a parallelogram ABCD intersect each other at point O. If OA = x + y, OC = 20, OD = x + 3 and OB = 18; find the values of x and y.
In a parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD
(ii) DE bisects ∠ADC and
(iii) Angle DEC is a right angle.
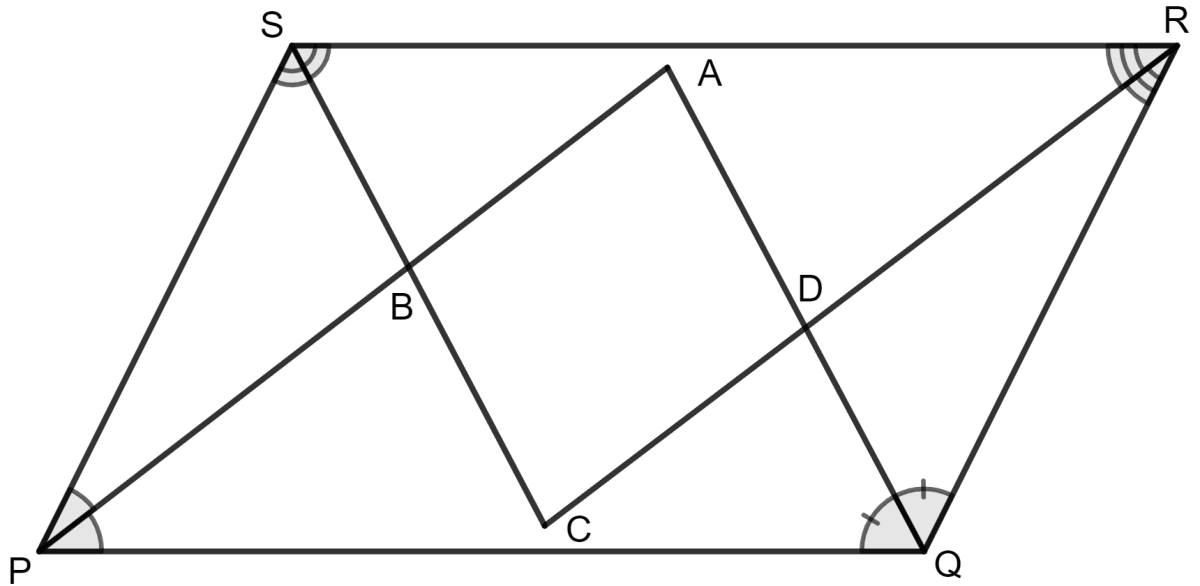
In the diagram given below, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD. Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle