Science
Make a diagram to show how hypermetropia is corrected. The near point of a hypermetropic eye is 1 m. What is the power of the lens required to correct this defect? Assume that the near point of the normal eye is 25 cm.
Human Eye
Answer
Hypermetropia can be corrected by using a convex lens as shown in the diagram below:
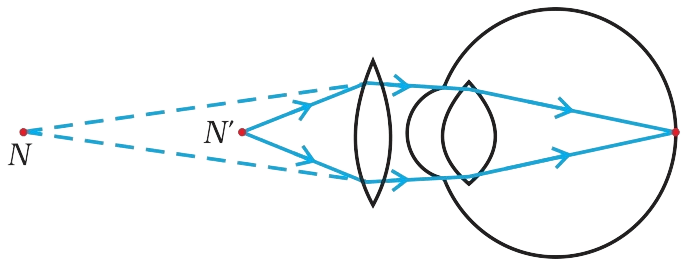
An object at 25 cm forms an image at the near point of hypermetropic eye.
Given,
Near point of hypermetropic eye = 1 m =100 cm
Object distance, u = -25 cm
Image distance, v = -100 cm
According to the formula,
Hence, the power of the lens required to correct this defect is 3 dioptre.
Answered By
Related Questions
A person needs a lens of power –5.5 dioptres for correcting his distant vision. For correcting his near vision he needs a lens of power +1.5 dioptre. What is the focal length of the lens required for correcting (i) distant vision, and (ii) near vision?
The far point of a myopic person is 80 cm in front of the eye. What is the nature and power of the lens required to correct the problem?
Why is a normal eye not able to see clearly the objects placed closer than 25 cm?
What happens to the image distance in the eye when we increase the distance of an object from the eye?