Locate $\sqrt{10}$ and $\sqrt{17}$ on the number line.

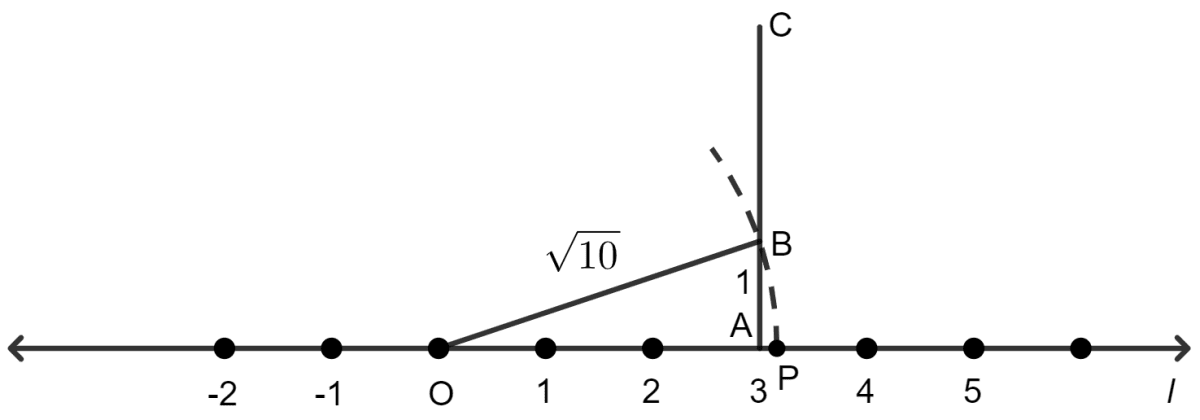
Locating $\sqrt{10}$:

Representing 10 as the sum of squares of two natural numbers:

10 = 9 + 1 = 3² + 1²

Let l be the number line. If point O represents number 0 and point A represents number 3, then draw a line segment OA = 3 units.

At A, draw AC ⟂ OA. From AC, cut off AB = 1 unit.

We observe that OAB is a right angled triangle at A. By Pythagoras theorem, we get:

$OB^2 = OA^2 + AB^2 \\[0.5em] \Rightarrow OB^2 = 3^2 + 1^2 \\[0.5em] \Rightarrow OB^2 = 9 + 1 \\[0.5em] \Rightarrow OB^2 = 10 \\[0.5em] \Rightarrow OB = \sqrt{10} \text{ units} \\[0.5em]$

With O as centre and radius = OB, we draw an arc of a circle to meet the number line l at point P.

As OP = OB = $\sqrt{10}$ units, the point P will represent the number $\sqrt{10}$ on the number line as shown in the figure below:

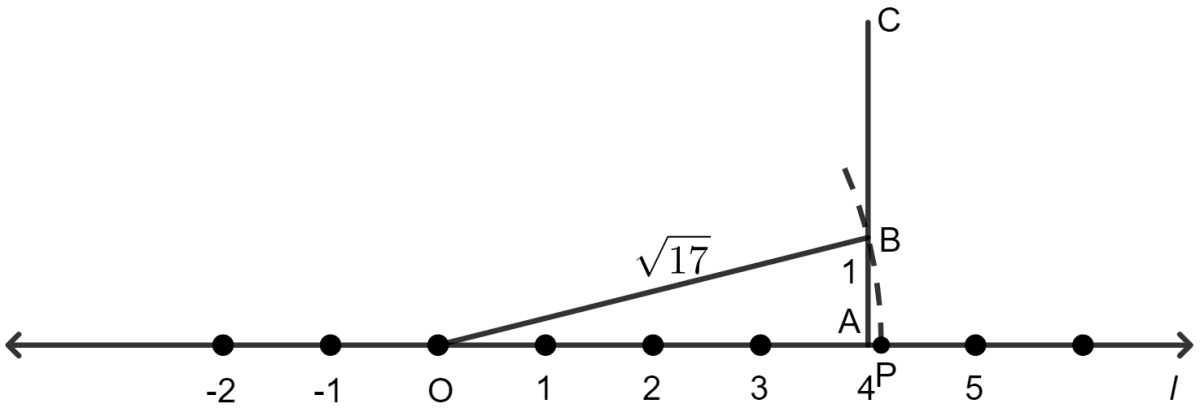
Locating $\sqrt{17}$:

Representing 17 as the sum of squares of two natural numbers:

17 = 16 + 1 = 4² + 1²

Let l be the number line. If point O represents number 0 and point A represents number 4, then draw a line segment OA = 4 units.

At A, draw AC ⟂ OA. From AC, cut off AB = 1 unit.

We observe that OAB is a right angled triangle at A. By Pythagoras theorem, we get:

$OB^2 = OA^2 + AB^2 \\[0.5em] \Rightarrow OB^2 = 4^2 + 1^2 \\[0.5em] \Rightarrow OB^2 = 16 + 1 \\[0.5em] \Rightarrow OB^2 = 17 \\[0.5em] \Rightarrow OB = \sqrt{17} \text{units} \\[0.5em]$

With O as centre and radius = OB, we draw an arc of a circle to meet the number line l at point P.

As OP = OB = $\sqrt{17}$ units, the point P will represent the number $\sqrt{17}$ on the number line as shown in the figure below: