Mathematics
It is given that △ABC ~ △PQR with , then is equal to
9
3
Similarity
3 Likes
Answer
Given
So, .
Since triangles are similar. We know that, the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.
Hence, Option 1 is the correct option.
Answered By
1 Like
Related Questions
In the adjoining figure, PQ || CA and all lengths are given in centimeters. The length of BC is

6.4 cm
7.4 cm
8 cm
9 cm
In the adjoining figure, MN || QR. If PN = 3.6 cm, NR = 2.4 cm and PQ = 5 cm, then PM is
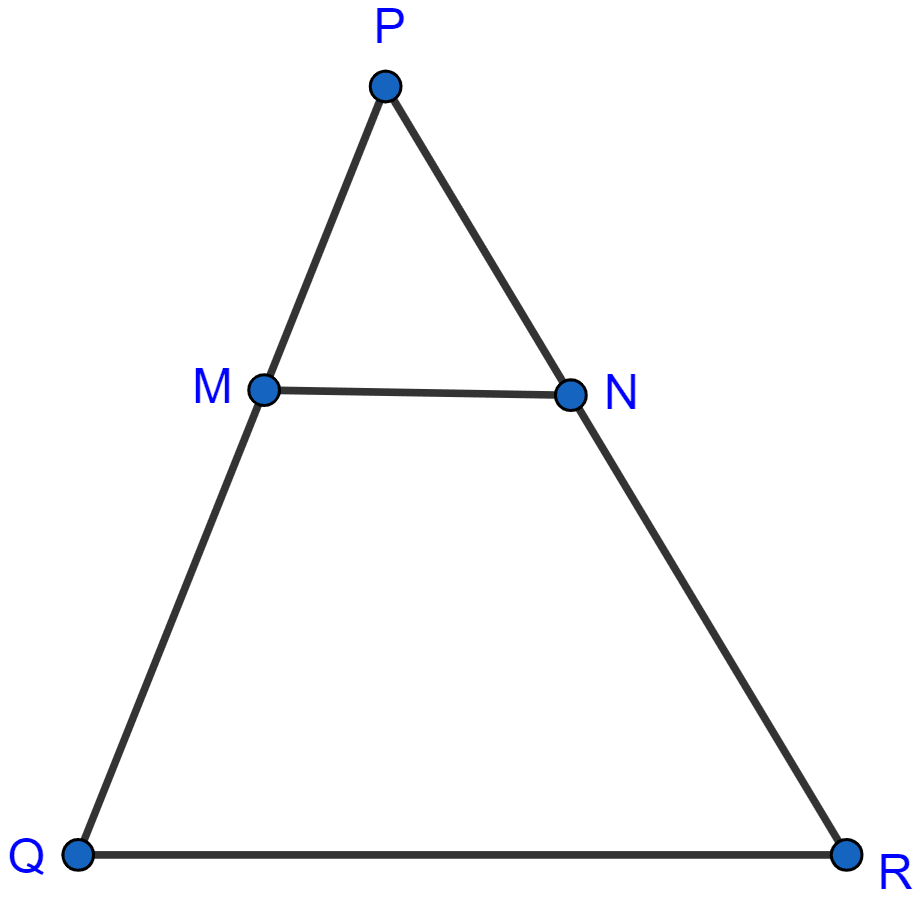
4 cm
3.6 cm
2 cm
3 cm
If the areas of two similar triangles are in the ratio 4 : 9, then their corresponding sides are in the ratio
9 : 4
3 : 2
2 : 3
16 : 81
If △ABC ~ △PQR, BC = 8 cm and QR = 6 cm, then the ratio of the areas of △ABC and △PQR is
8 : 6
3 : 4
9 : 16
16 : 9