Mathematics
In triangle LMN, bisectors of interior angles at L and N intersect each other at point A. Prove that:
(i) point A is equidistant from all the three sides of the triangle.
(ii) AM bisects angle LMN.
Answer
Steps of construction :
Construct a triangle LMN.
Draw angle bisectors of L and N. Let the angle bisectors meet at A.
Join AM.
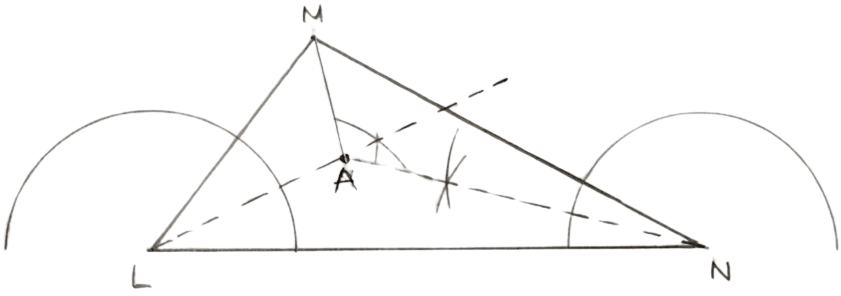
(i) Since, A lies on bisector of ∠N
∴ A is equidistant from MN and LN.
Again, as A lies on the bisector of ∠L
∴ A is equidistant from LN and LM.
Hence, proved that A is equidistant from all three sides of the triangle LMN.
(ii) From above part we get,
A is equidistant from MN and LN and also from LN and LM.
We get,
A is equidistant from MN and LM.
∴ A lies on angle bisector of ∠LMN.
Hence, proved that AM bisects ∠LMN.
Related Questions
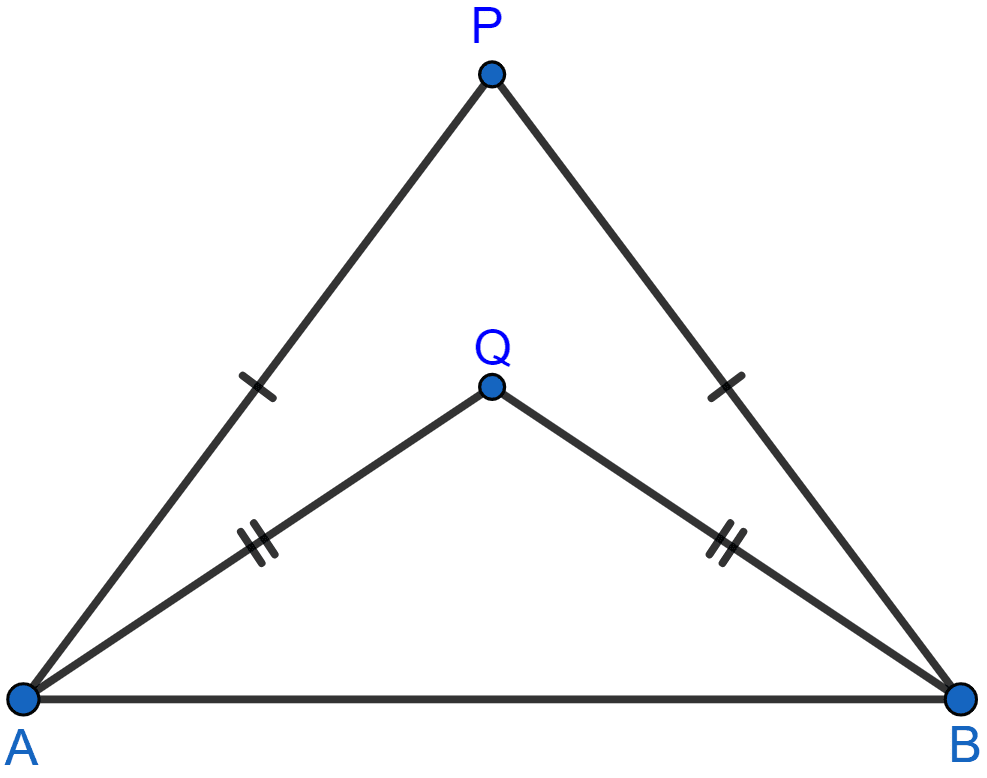
In each of the given figures; PA = PB and QA = QB.
(i)
(ii)
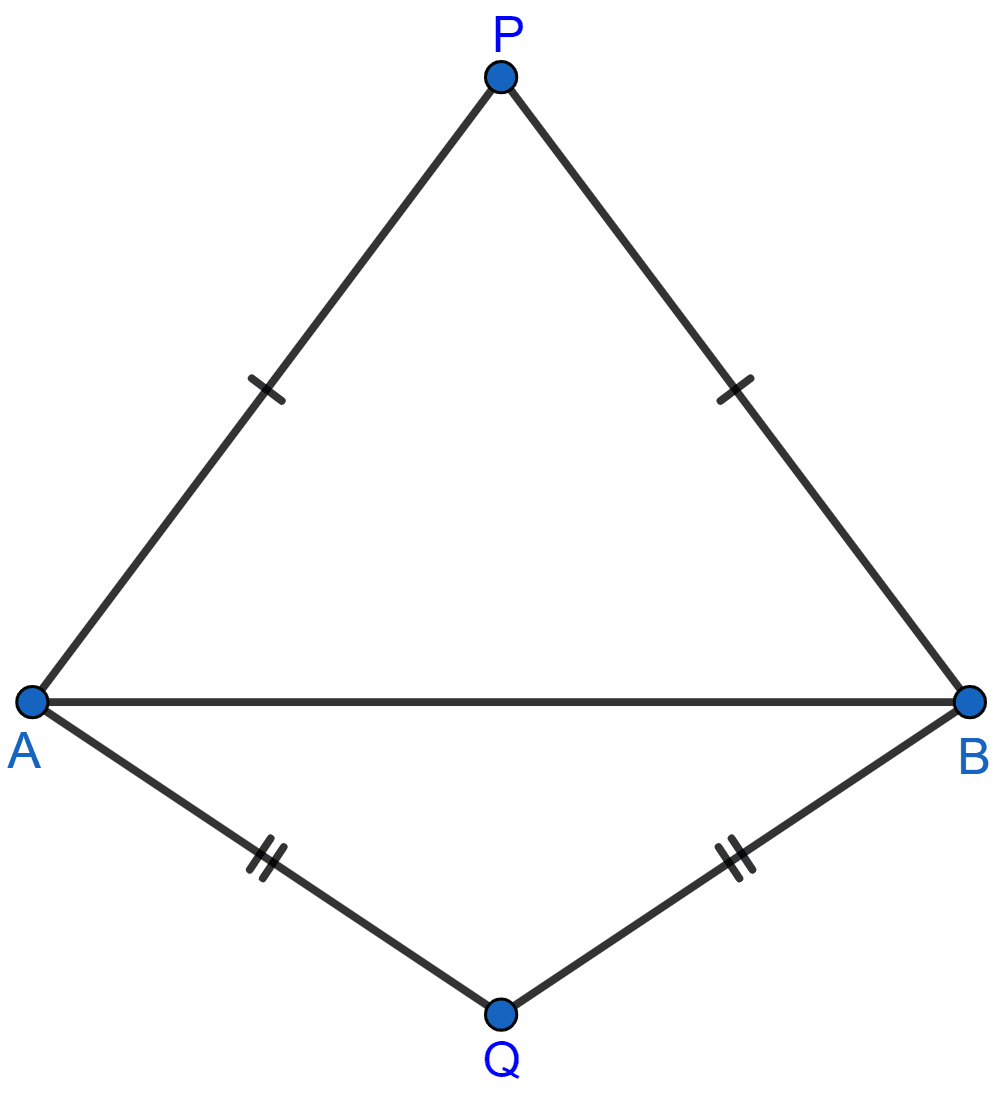
Prove in each case, that PQ (produce, if required) is perpendicular bisector of AB.
Hence, state the locus of the points equidistant from two given fixed points.
Construct a triangle ABC in which angle ABC = 75°, AB = 5 cm and BC = 6.4 cm. Draw perpendicular bisector of side BC and also the bisector of angle ACB. If these bisectors intersect each other at point P; prove that P is equidistant from B and C; and also from AC and BC.
In parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B. Prove that P is equidistant from AB and BC.
Use ruler and compasses only for this question.
(i) Construct △ABC, where AB = 3.5 cm, BC = 6 cm and ∠ABC = 60°.
(ii) Construct the locus of points inside the triangle which are equidistant from BA and BC.
(iii) Construct the locus of points inside the triangle which are equidistant from B and C.
(iv) Mark the point P which is equidistant from AB, BC and also equidistant from B and C. Measure and record the length of PB.