Mathematics
In triangle ABC, D is a point in AB such that AC = CD = DB. If ∠B = 28°, find the angle ACD.
Triangles
1 Like
Answer
Given,
∠B = 28°
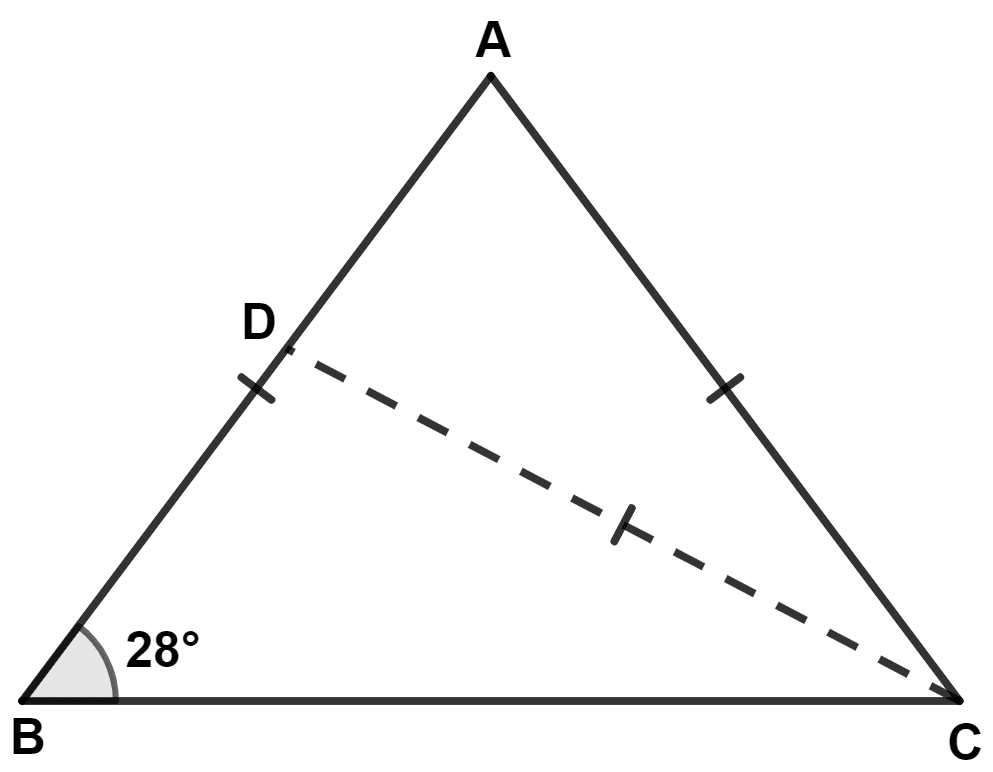
From figure,
DBC is an isosceles triangle, with DB = DC.
∴ ∠DCB = ∠DBC = 28° (Angles opposite to equal sides are equal)
In △ DBC,
By angle sum property of triangle,
⇒ ∠DCB + ∠DBC + ∠BDC = 180°
⇒ 28° + 28° + ∠BDC = 180°
⇒ 56° + ∠BDC = 180°
⇒ ∠BDC = 180° - 56° = 124°.
From figure,
ADB is a straight line.
∴ ∠ADC + ∠BDC = 180°
⇒ ∠ADC = 180° - ∠BDC = 180° - 124° = 56°.
Since, ADC is an isosceles triangle with AC = DC.
⇒ ∠ADC = ∠DAC = 56° (Angles opposite to equal sides are equal)
By angle sum property of triangle,
⇒ ∠ADC + ∠DAC + ∠ACD = 180°
⇒ 56° + 56° + ∠ACD = 180°
⇒ ∠ACD + 112° = 180°
⇒ ∠ACD = 180° - 112° = 68°.
Hence, ∠ACD = 68°.
Answered By
1 Like
Related Questions
In quadrilateral ABCD, side AB is the longest and side DC is the shortest. Prove that :
(i) ∠C > ∠A
(ii) ∠D > ∠B
In triangle ABC, side AC is greater than side AB. If the internal bisector of angle A meets the opposite side at point D, prove that : ∠ADC is greater than ∠ADB.
In isosceles triangle ABC, sides AB and AC are equal. If point D lies in base BC and point E lies on BC produced (BC being produced through vertex C), prove that :
(i) AC > AD
(ii) AE > AC
(iii) AE > AD
Given : ED = EC
Prove : AB + AD > BC.