Mathematics
In triangle ABC, AB = AC and BD is perpendicular to AC. Prove that :
BD2 - CD2 = 2CD × AD
Pythagoras Theorem
15 Likes
Answer
By formula,
By pythagoras theorem,
⇒ (Hypotenuse)2 = (Perpendicular)2 + Base2
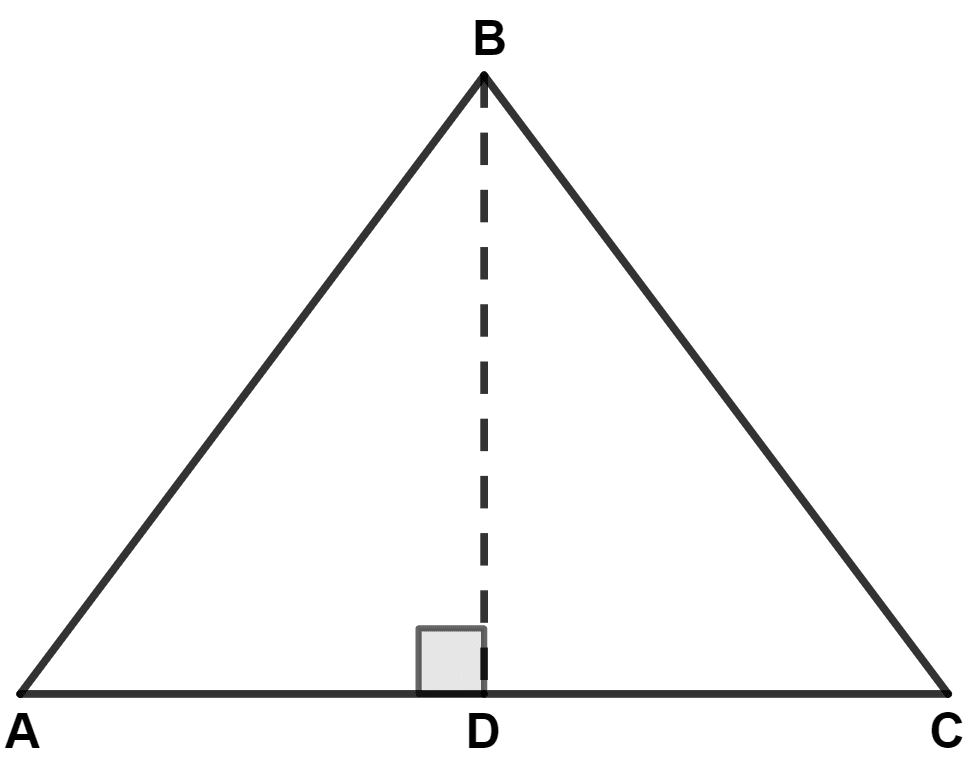
In right-angled triangle ABD,
By pythagoras theorem,
⇒ AB2 = AD2 + BD2
⇒ AD2 = AB2 - BD2 …….(1)
From figure,
⇒ AC = AD + DC
Squaring both sides, we get :
⇒ AC2 = (AD + DC)2
⇒ AC2 = AD2 + DC2 + 2AD.DC
⇒ AC2 = AB2 - BD2 + DC2 + 2AD.DC [From equation (1)]
Substituting AB = AC, in above equation :
⇒ AC2 = AC2 - BD2 + DC2 + 2AD.DC
⇒ AC2 - AC2 + BD2 - DC2 = 2AD.DC
⇒ BD2 - DC2 = 2CD × AD.
Hence, proved that BD2 - DC2 = 2CD × AD.
Answered By
10 Likes
Related Questions
In an isosceles triangle ABC; AB = AC and D is a point on BC produced. Prove that :
AD2 = AC2 + BD.CD
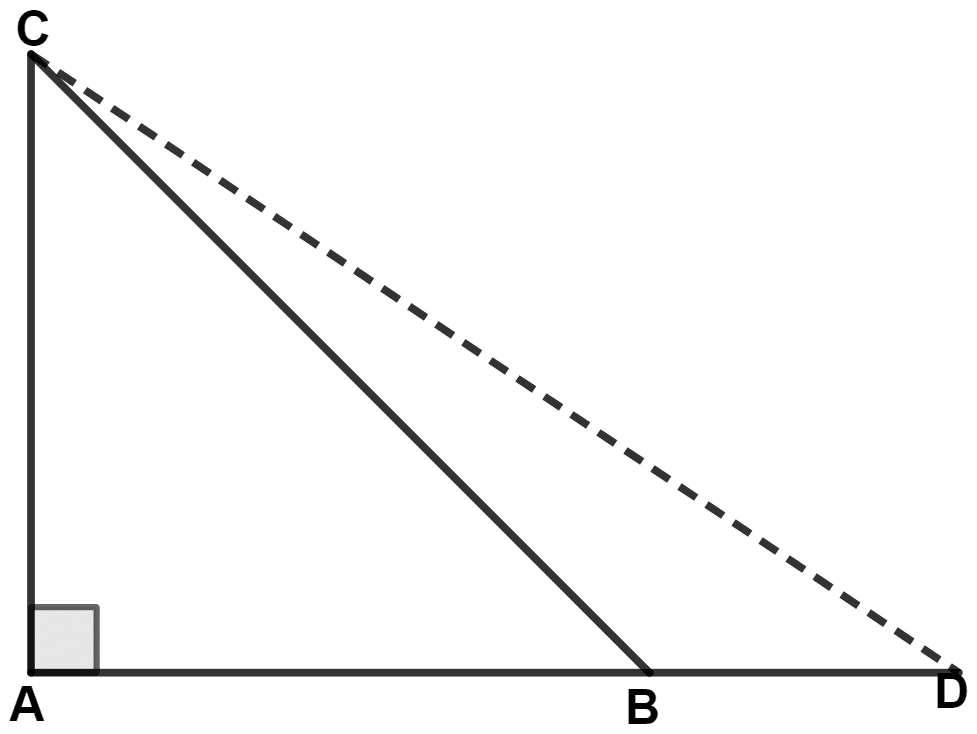
In triangle ABC, angle A = 90°, CA = AB and D is a point on AB produced. Prove that :
DC2 - BD2 = 2AB.AD.
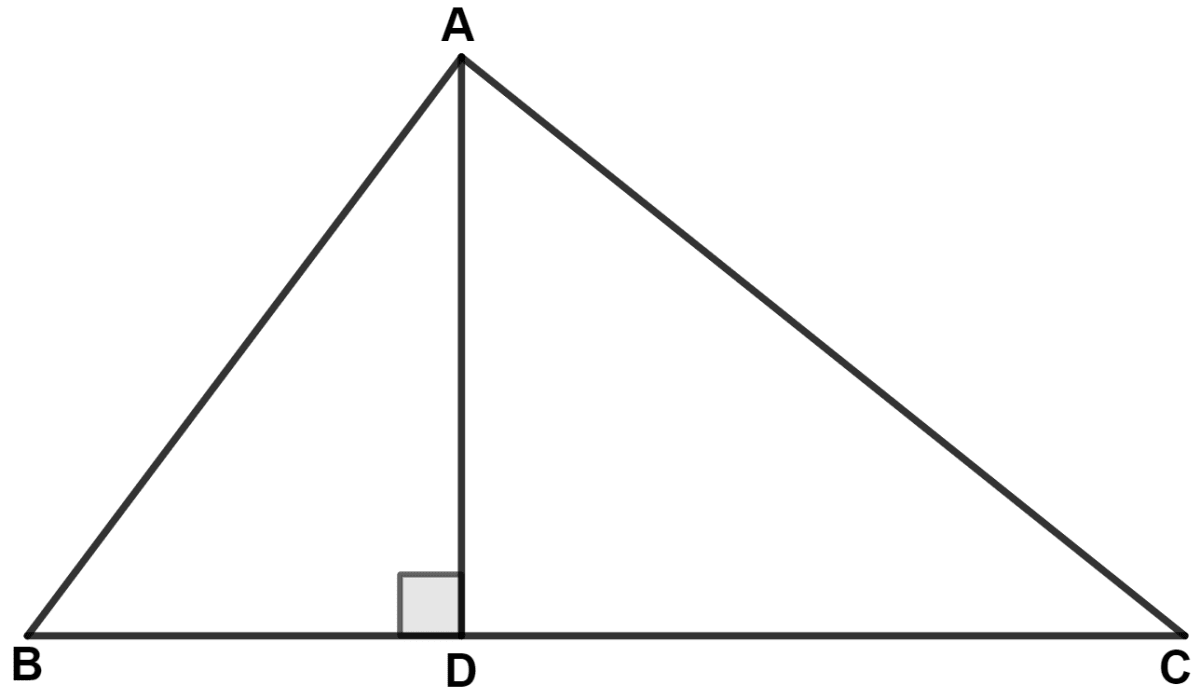
In the following figure, AD is perpendicular to BC and D divides BC in the ratio 1 : 3.
Prove that : 2AC2 = 2AB2 + BC2.
In the given figure, AB = 16 cm, BC = 12 cm and CA = 6 cm; find the length of CD.