Mathematics
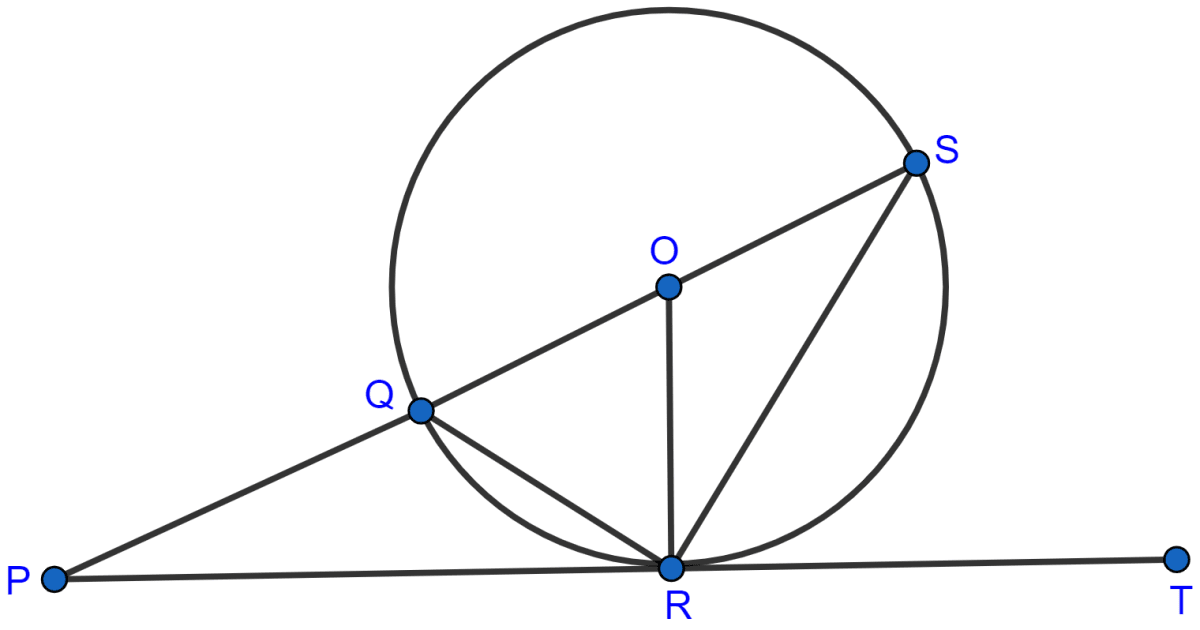
In the given figure, PT touches the circle with center O at point R. Diameter SQ is produced to meet the tangent TR at P.
Given ∠SPR = x° and ∠QRP = y°;
prove that :
(i) ∠ORS = y°
(ii) write an expression connecting x and y.
Circles
Answer
(i) From figure,
⇒ ∠QRP = ∠OSR = y° [Angles in alternate segment are equal]
⇒ OS = OR (Radius of same circle)
As, angles opposite to equal sides are equal,
∴ ∠ORS = ∠OSR = y°.
Hence, proved that ∠ORS = y°.
(ii) From figure,
∠ORP = 90° [As, tangent to a point and radius from that point are perpendicular to each other.]
⇒ ∠ORQ = ∠ORP - ∠QRP = 90° - y° ………..(1)
OQ = OR (Radius of same circle)
As, angles opposite to equal sides are equal,
∴ ∠OQR = ∠ORQ = 90° - y°
In △PQR,
⇒ ∠OQR = ∠QPR + ∠QRP (As exterior angle in a trinagle is equal to the sum of two opposite interior angles.)
⇒ 90° - y° = x° + y°
⇒ x° + 2y° = 90°.
Hence, x + 2y = 90°.
Answered By
Related Questions
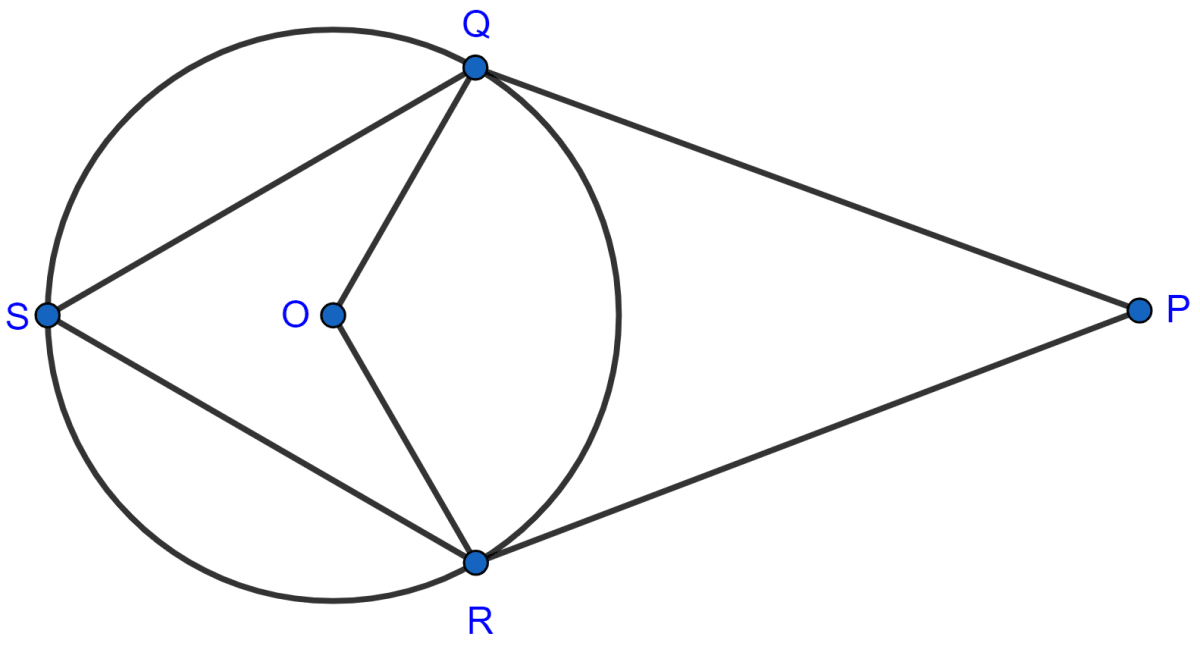
In the following figure, PQ and PR are tangents to the circle, with center O. If ∠QPR = 60°, calculate :
(i) ∠QOR,
(ii) ∠OQR,
(iii) ∠QSR.
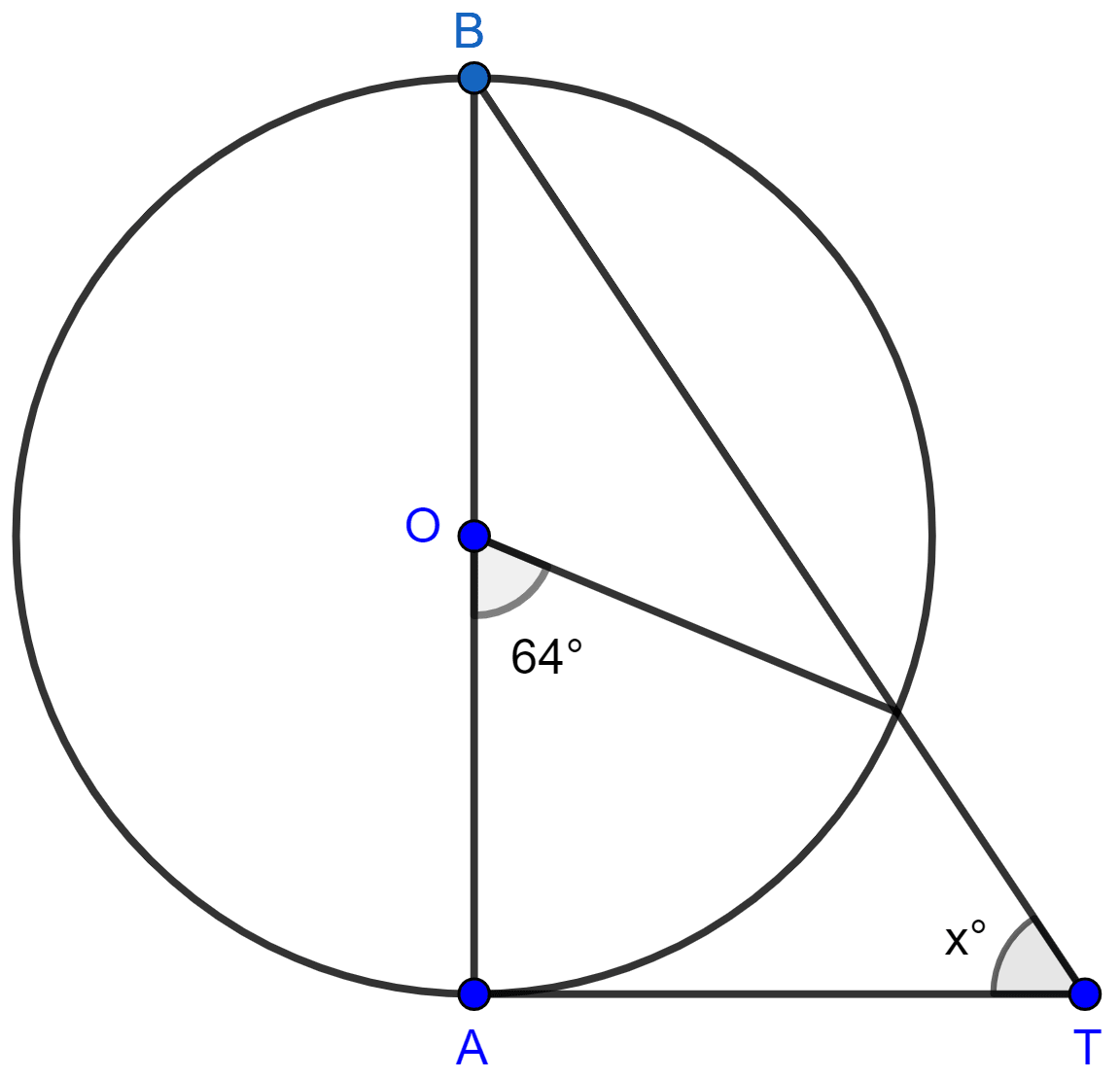
In the given figure, AB is the diameter of the circle, with center O, and AT is the tangent. Calculate the numerical value of x.
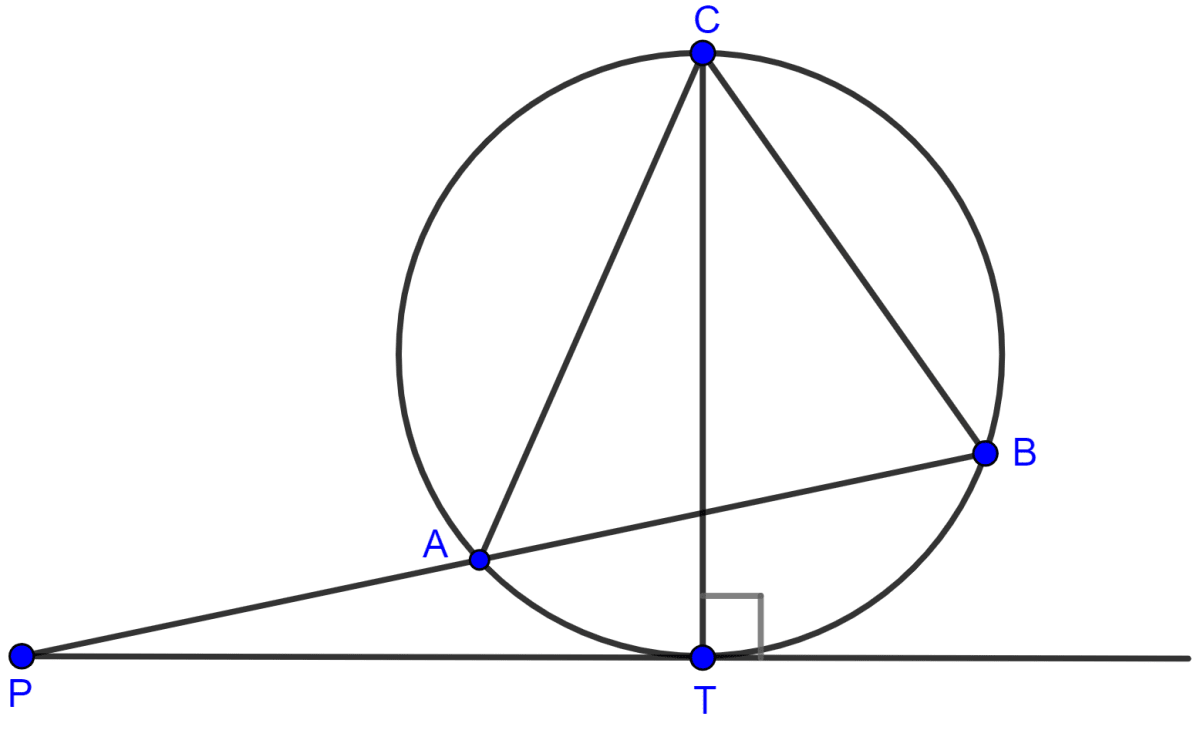
PT is a tangent to the circle at T. If ∠ABC = 70° and ∠ACB = 50°; calculate :
(i) ∠CBT
(ii) ∠BAT
(iii) ∠APT
In the given figure, O is the center of the circumcircle ABC. Tangents A and C intersect at P. Given angle AOB = 140° and angle APC = 80°; find the angle BAC.
