Mathematics
In the given figure, O is the center of the circumcircle of triangle XYZ. Tangents at points X and Y intersect at point T. If angle XTY = 80° and angle XOZ = 140°, find the angle ZXY.
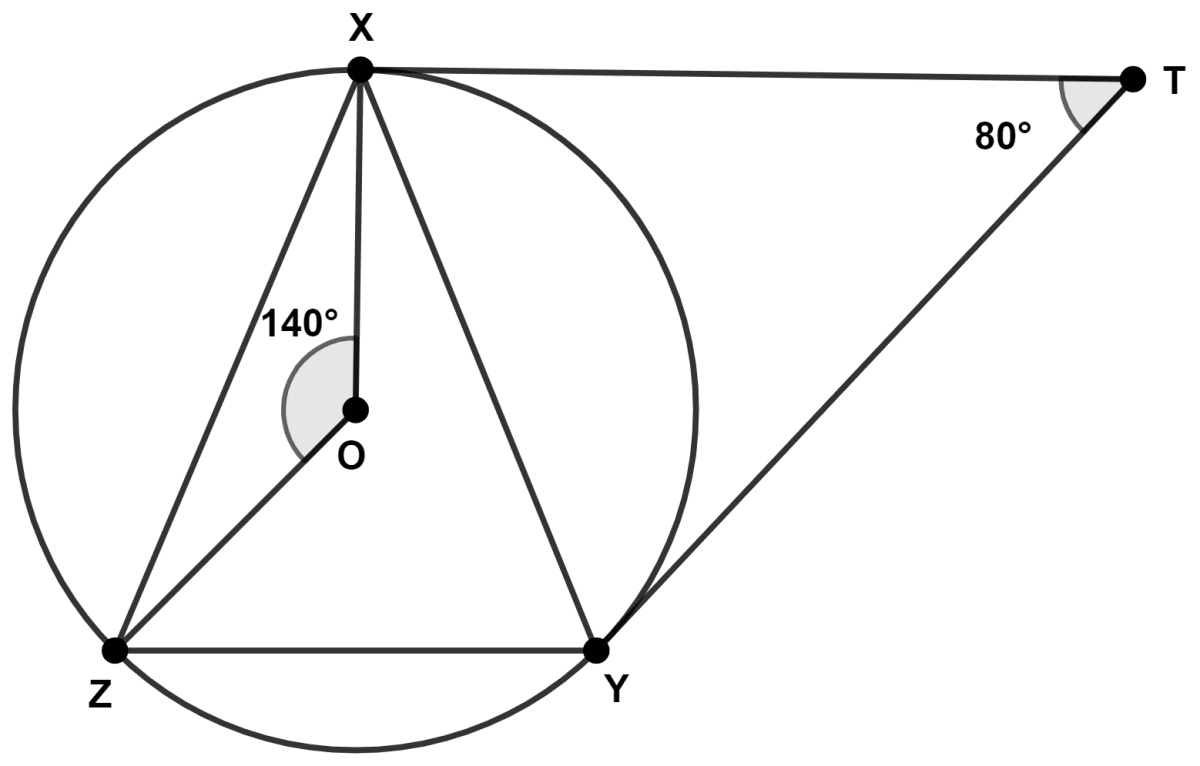
Circles
3 Likes
Answer
Join OY.
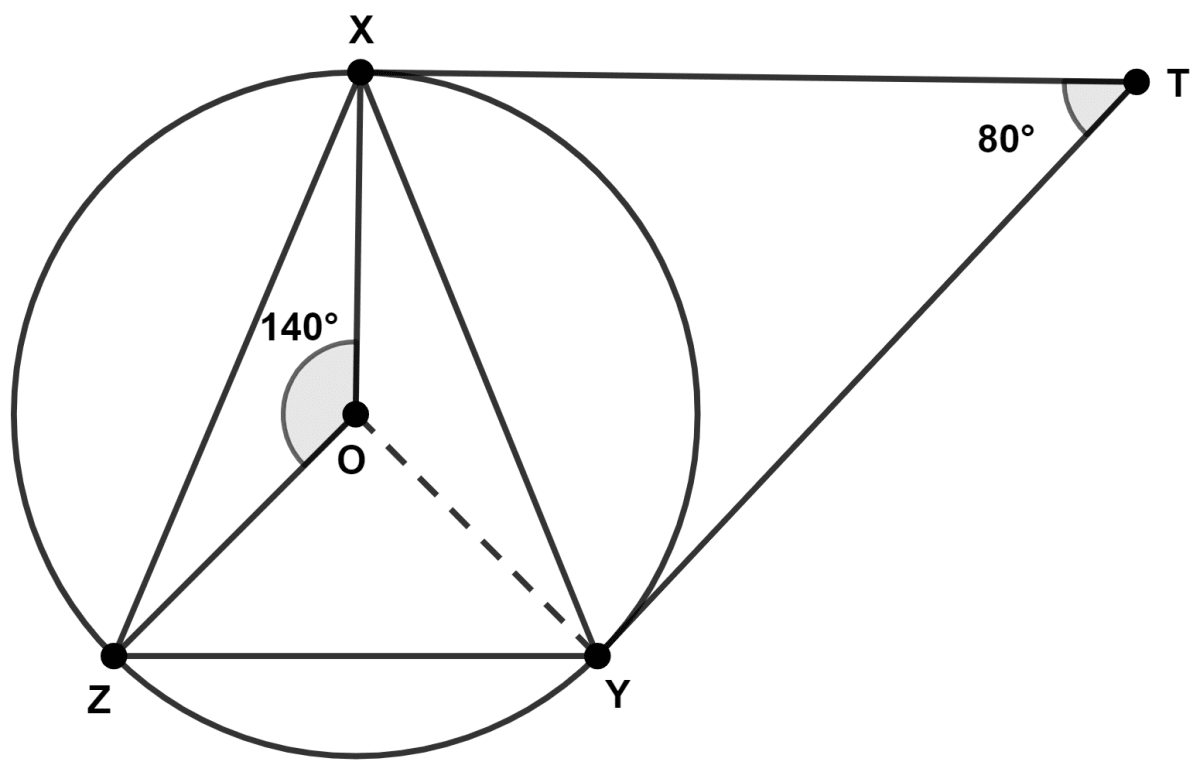
Since a tangent at any point of a circle is perpendicular to the radius at the point of contact, we have
∠OXT = ∠OYT = 90°.
Since sum of angles of a quadrilateral is 360°.
In XOYT,
⇒ ∠OXT + ∠OYT + ∠XOY + ∠XTY = 360°
⇒ 90° + 90° + ∠XOY + 80° = 360°
⇒ ∠XOY = 360° - 90° - 90° - 80° = 100°.
From figure,
⇒ ∠XOY + ∠XOZ + ∠ZOY = 360°
⇒ 100° + 140° + ∠ZOY = 360°
⇒ ∠ZOY = 360° - 100° - 140° = 120°.
We know that,
Angle subtended by an arc on the center of circle is twice the angle subtended by it on any part of the circumference.
∴ 2∠ZXY = ∠ZOY
⇒ ∠ZXY = = 60°.
Hence, ∠ZXY = 60°.
Answered By
1 Like
Related Questions
Find the set of values of x satisfying 7x + 3 ≥ 3x - 5 and ∈ N.
Cards numbered 11 to 60 are kept in a box. If a card is drawn at random from the box, find the probability that the number on the drawn card is :
(i) a perfect square number
(ii) divisible by 5
(iii) a prime number less than 20.
Using assumed mean method, calculate the mean.
Class-interval Frequency 0-30 22 30-60 30 60-90 40 90-120 36 120-150 28 150-180 20 A cylindrical vessel with internal diameter 10 cm and height 10.5 cm is full of water. A solid cone of base diameter 7 cm and height 6 cm is completely immersed in water in the vessel. Find the volume of water left in the cylinder.
(Take )