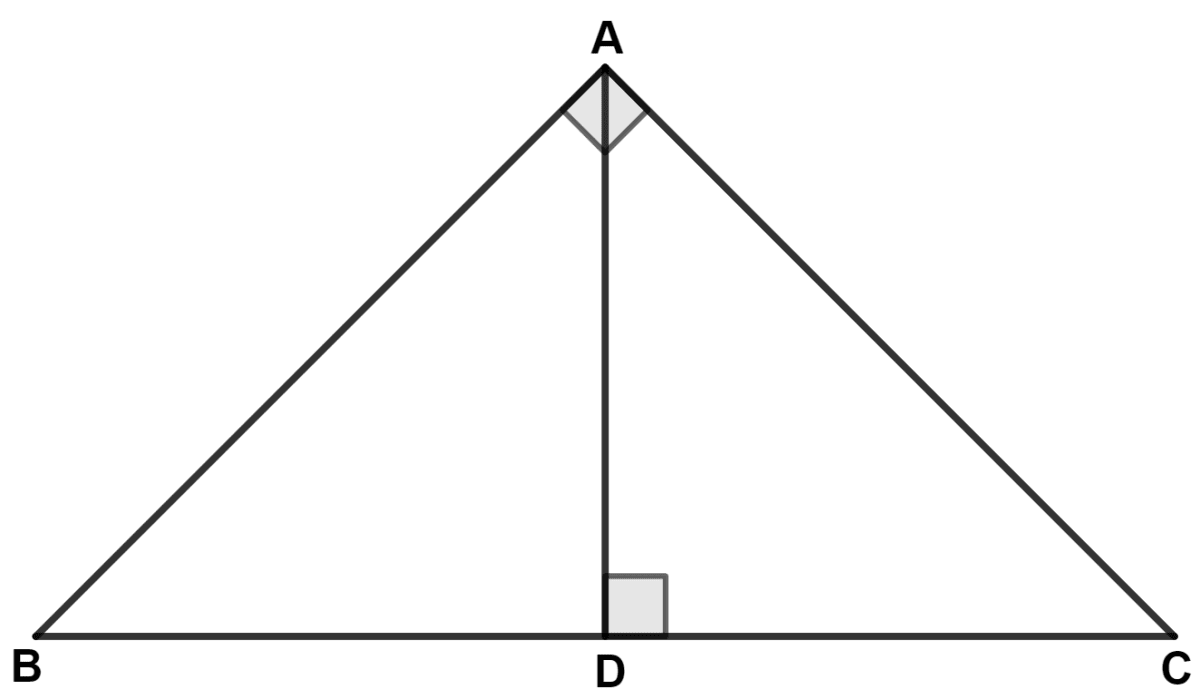
In the given figure, ∠BAC = 90°, AD is perpendicular to BC, BC = 13 cm and AC = 5 cm, then area of △ ADC : area of △ DBA is :

1. 5 : 13

2. 13 : 5

3. 25 : 144

4. 144 : 25

From figure,

In Δ BAC and Δ ADC,

⇒ ∠BAC = ∠ADC (Both equal to 90°)

⇒ ∠ACB = ∠ACD (Common angle)

∴ Δ BAC ~ Δ ADC (By A.A. postulate)

We know that,

The areas of two similar triangles are proportional to the squares of their corresponding sides.

$\therefore \dfrac{\text{Area of Δ BAC}}{\text{Area of Δ ADC}} = \dfrac{BC^2}{AC^2} \\[1em] \Rightarrow \dfrac{\text{Area of Δ BAC}}{\text{Area of Δ ADC}} = \dfrac{13^2}{5^2} \\[1em] \Rightarrow \dfrac{\text{Area of Δ BAC}}{\text{Area of Δ ADC}} = \dfrac{169}{25}.$

Let, area of Δ BAC = 169x and area of Δ ADC = 25x.

From figure,

Area of Δ DBA = Area of Δ BAC - Area of Δ ADC = 169x - 25x = 144x.

Substituting values we get :

area of △ ADC : area of △ DBA = 25x : 144x = 25 : 144.

Hence, Option 3 is the correct option.