Mathematics
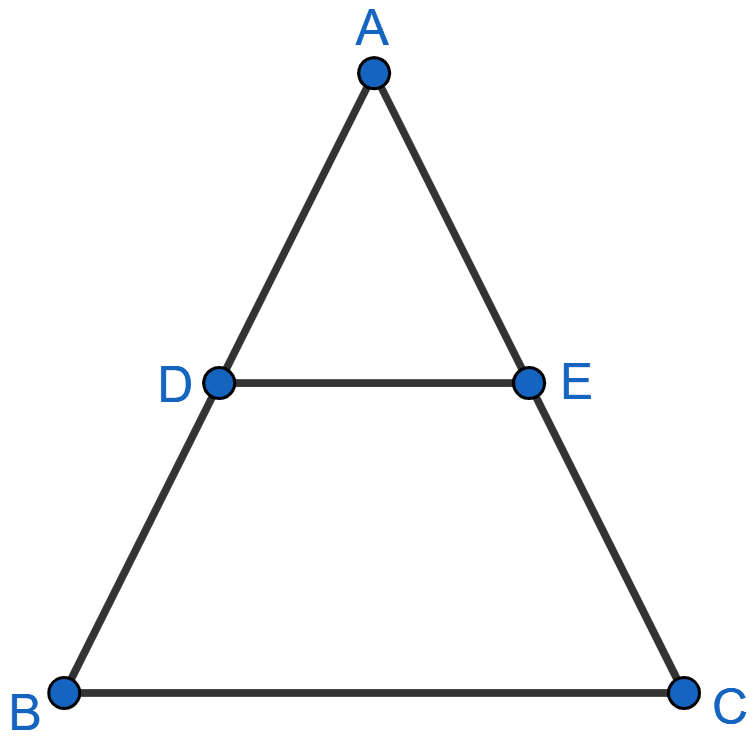
In the given figure, ΔABC ~ ΔADE. If AE : EC = 4 : 7 and DE = 6.6 cm, find BC. If 'x' be the length of the perpendicular from A to DE, find the length of perpendicular from A to BC in terms of 'x'.
Similarity
16 Likes
Answer
Given,
ΔABC ~ ΔADE
Given,
AE : EC = 4 : 7
Let AE = 4y and EC = 7y.
So, AC = 4y + 7y = 11y.
From figure,
Since, corresponding sides of similar triangles are proportional we have :
As ΔABC ~ ΔADE, we have :
∠ABC = ∠ADE and ∠ACB = ∠AED
So, DE || BC as ∠ADE and ∠ABC are corresponding angles.
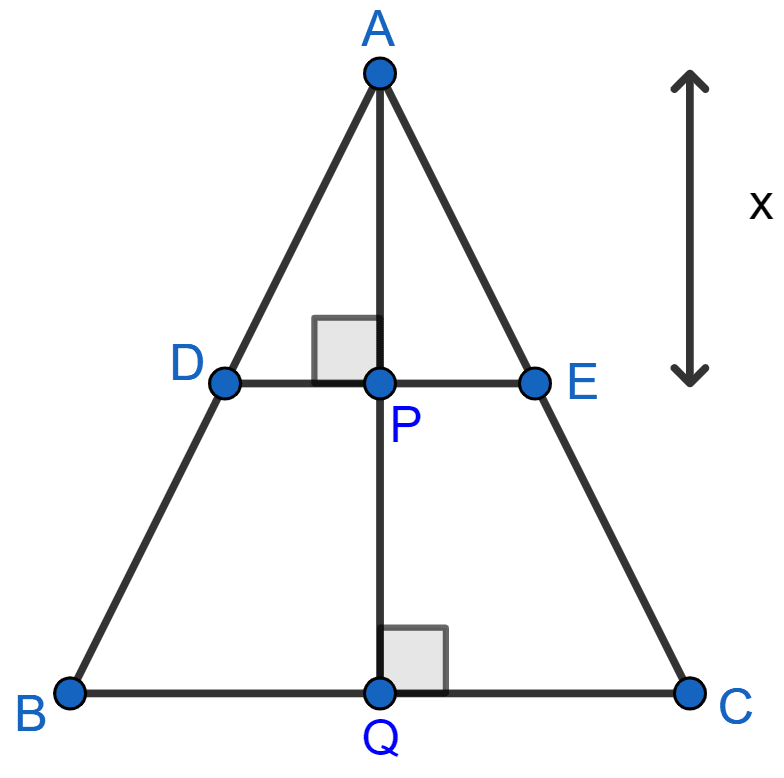
Let perpendicular from A to DE meet DE at point P. Then,
AP = x
Let perpendicular from A to BC meet BC at point Q.
In ∆ADP and ∆ABQ,
∠ADP = ∠ABQ [Corresponding angles are equal.]
∠APD = ∠AQB [Both = 90°]
∴ ∆ADP ~ ∆ABQ [By AA]
Hence, BC = 18.15 cm and AQ =
Answered By
9 Likes
Related Questions
A line PQ is drawn parallel to the side BC of ΔABC which cuts side AB at P and side AC at Q. If AB = 9.0 cm, CA = 6.0 cm and AQ = 4.2 cm, find the length of AP.
In ΔABC, D and E are the points on sides AB and AC respectively.
Find whether DE || BC, if
(i) AB = 9 cm, AD = 4 cm, AE = 6 cm and EC = 7.5 cm.
(ii) AB = 6.3 cm, EC = 11.0 cm, AD = 0.8 cm and EA = 1.6 cm.
A line segment DE is drawn parallel to base BC of ∆ABC which cuts AB at point D and AC at point E. If AB = 5BD and EC = 3.2 cm, find the length of AE.
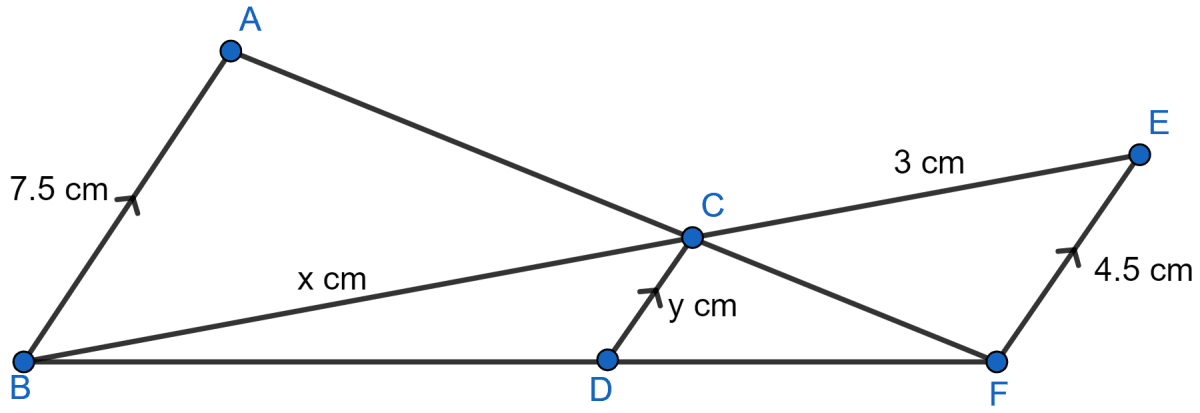
In the figure, given below, AB, CD and EF are parallel lines. Given AB = 7.5 cm, DC = y cm, EF = 4.5 cm, BC = x cm and CE = 3 cm, calculate the values of x and y.