Mathematics
In the given figure, AB is the diameter of the circle with centre O.
If ∠ADC = 32°, find angle BOC.

Answer
We know that,
Angle at the centre is twice the angle at remaining circumference.
Arc AC subtends ∠AOC at the centre and ∠ADC at the remaining part of the circle.
⇒ ∠AOC = 2∠ADC
⇒ ∠AOC = 2 x 32° = 64°
From figure,
∠AOC and ∠BOC are linear pair,
∴ ∠AOC + ∠BOC = 180°
⇒ 64° + ∠BOC = 180°
⇒ ∠BOC = 180° - 64° = 116°.
Hence, ∠BOC = 116°.
Related Questions
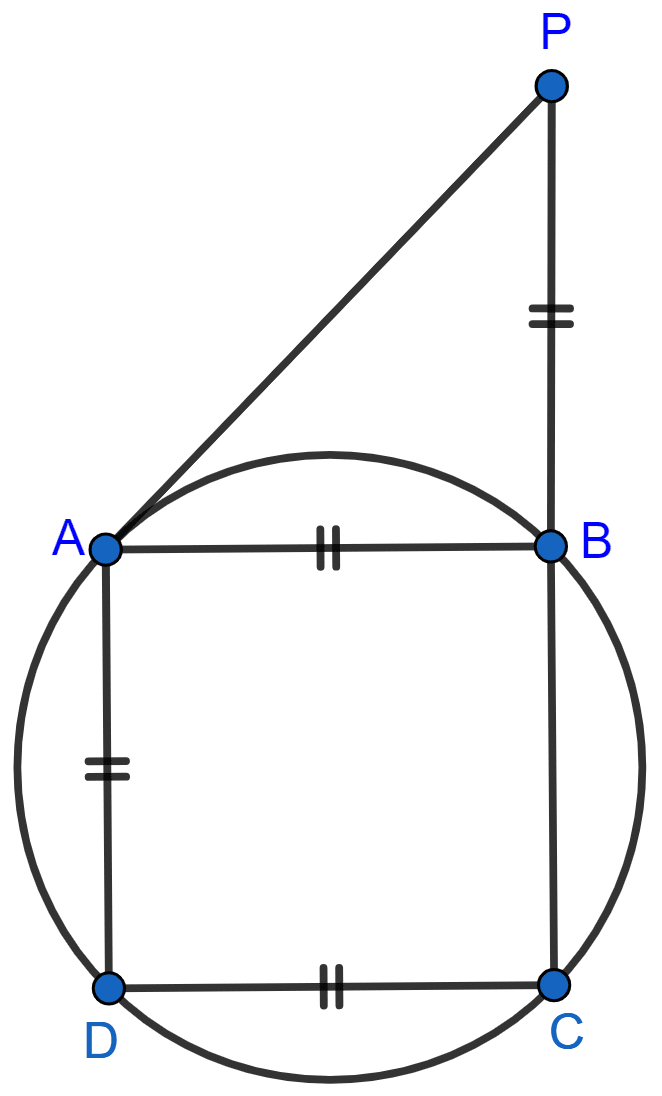
In the given figure, AB = AD = DC = PB and ∠DBC = x°. Determine, in terms of x :
(i) ∠ABD, (ii) ∠APB.
Hence or otherwise, prove that AP is parallel to DB.
In a cyclic quadrilateral PQRS, angle PQR = 135°. Sides SP and RQ produced meet at point A whereas sides PQ and SR produced meet at point B.
If ∠A : ∠B = 2 : 1, find angles A and B.
In the following figure, ABCD is a cyclic quadrilateral in which AD is parallel to BC. If the bisector of angle A meets BC at point E and the given circle at point F, prove that :
(i) EF = FC
(ii) BF = DF

In the given figure; ABC, AEQ and CEP are straight lines. Show that ∠APE and ∠CQE are supplementary.