Mathematics
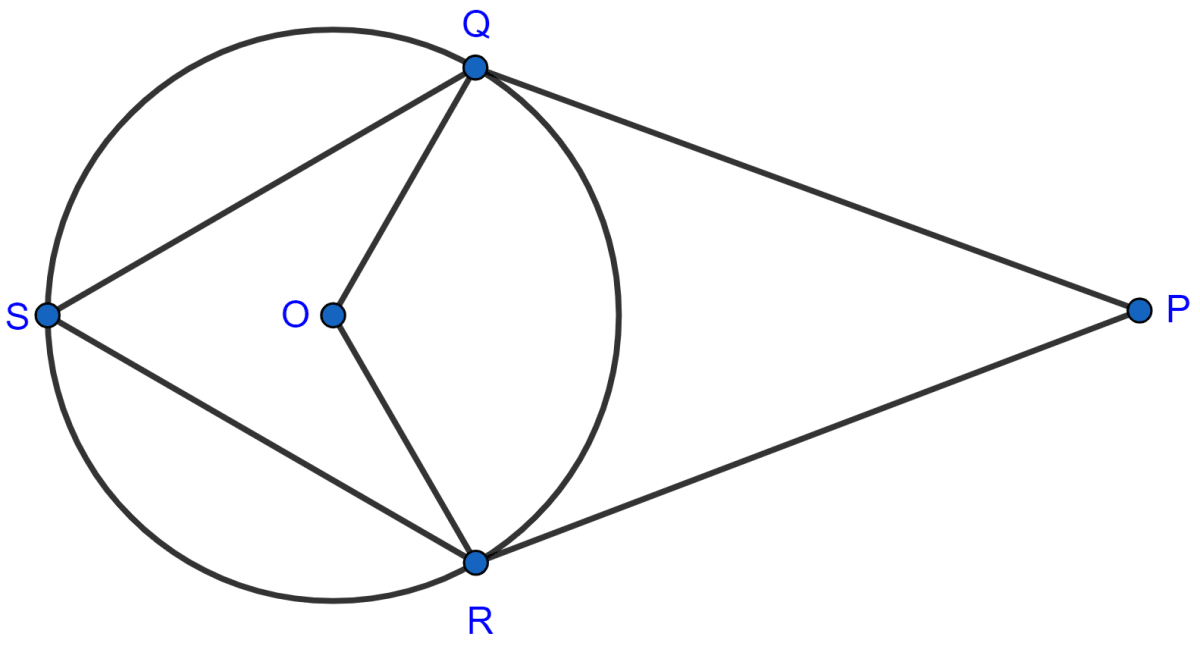
In the following figure, PQ and PR are tangents to the circle, with center O. If ∠QPR = 60°, calculate :
(i) ∠QOR,
(ii) ∠OQR,
(iii) ∠QSR.
Circles
Answer
(i) We know that,
The tangent at any point of a circle and the radius through this point are perpendicular to each other.
In quadrilateral ORPQ,
∠OQP = ∠ORP = 90° [∵ The tangent at any point of a circle and the radius through this point are perpendicular to each other]
∠QPR = 60° [Given]
⇒ ∠OQP + ∠ORP + ∠QPR + ∠QOR = 360° [By angle sum property of quadrilateral]
⇒ 90° + 90° + 60° + ∠QOR = 360°
⇒ 240° + ∠QOR = 360°
⇒ ∠QOR = 120°.
Hence, ∠QOR = 120°.
(ii) Join QR.
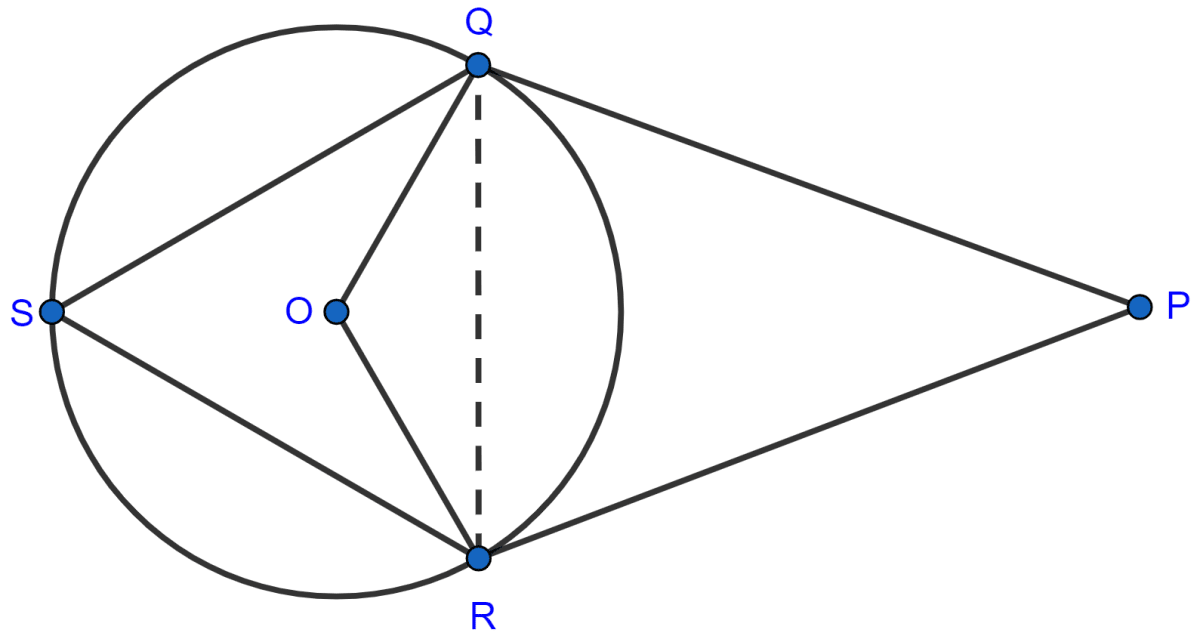
In △QOR,
OQ = OR (Radii of same circle)
As, angles opposite to equal sides are equal.
∴ ∠OQR = ∠ORQ ……….(1)
⇒ ∠OQR + ∠ORQ + ∠QOR = 180°
⇒ ∠OQR + ∠ORQ + 120° = 180°
⇒ ∠OQR + ∠ORQ = 180° - 120°
⇒ ∠OQR + ∠ORQ = 60°
⇒ ∠OQR + ∠OQR = 60°
⇒ 2∠OQR = 60°
⇒ ∠OQR =
⇒ ∠OQR = 30°.
Hence, ∠OQR = 30°.
(iii) Arc RQ subtends ∠QOR at the center and ∠QSR at the remaining part of the circle.
We know that,
The angle subtended by an arc at the centre is twice the angle subtended at the circumference.
⇒ ∠QOR = 2∠QSR
⇒ ∠QSR = ∠QOR = = 60°.
Hence, ∠QSR = 60°.
Answered By
Related Questions
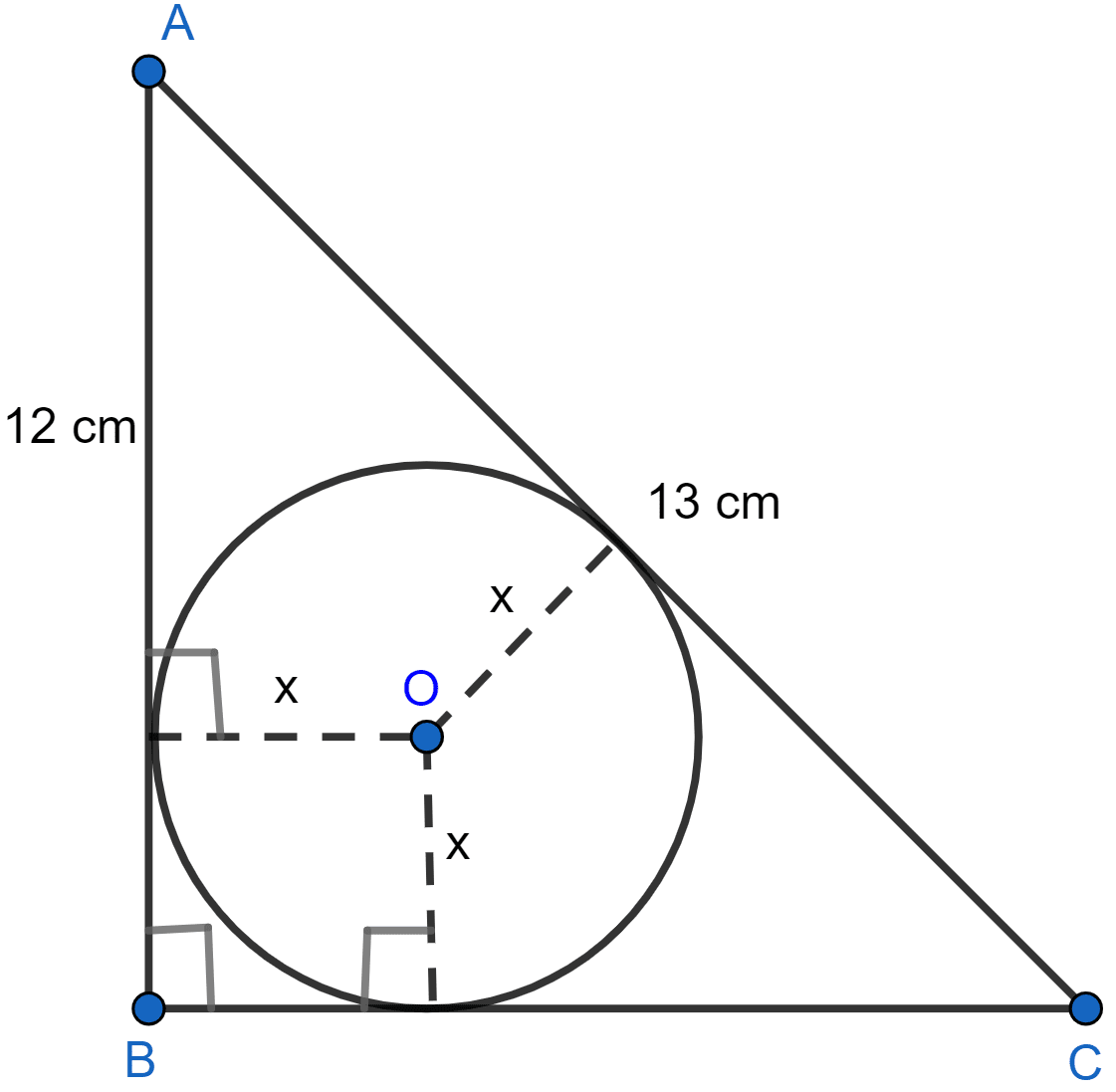
ABC is a right angled triangle with AB = 12 cm and AC = 13 cm. A circle, with center O, has been inscribed inside the triangle. Calculate the value of x, the radius of the inscribed circle.
In a triangle ABC, the incircle (center O) touches BC, CA and AB at points P, Q and R respectively. Calculate :
(i) ∠QOR
(ii) ∠QPR;
given that ∠A = 60°.
In the given figure, AB is the diameter of the circle, with center O, and AT is the tangent. Calculate the numerical value of x.
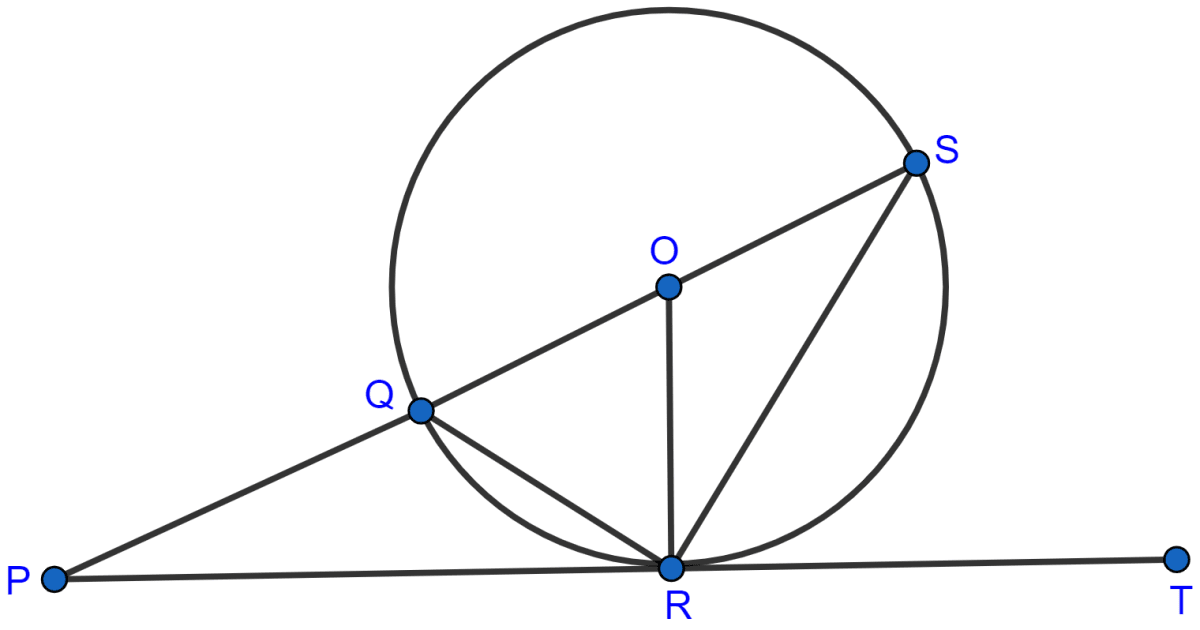
In the given figure, PT touches the circle with center O at point R. Diameter SQ is produced to meet the tangent TR at P.
Given ∠SPR = x° and ∠QRP = y°;
prove that :
(i) ∠ORS = y°
(ii) write an expression connecting x and y.