Mathematics
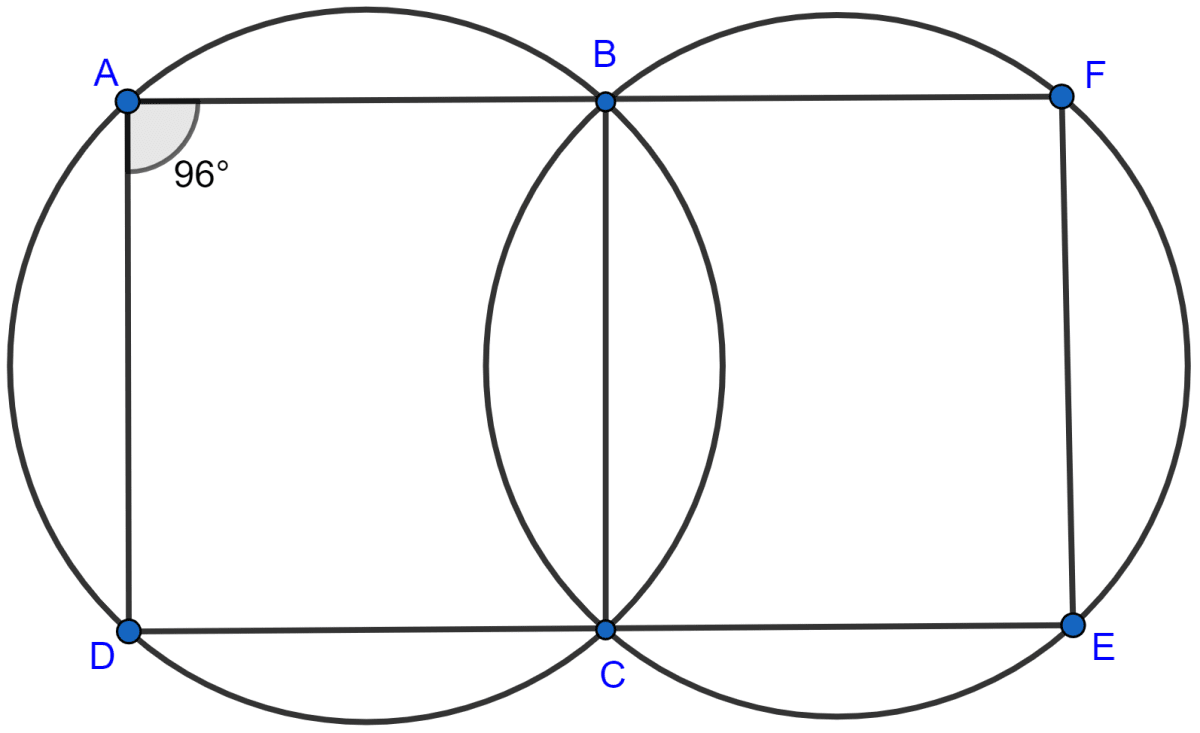
In the following figure,
(i) if ∠BAD = 96°, find ∠BCD and ∠BFE.
(ii) Prove that AD is parallel to FE.
Circles
13 Likes
Answer
(i) ABCD is a cyclic quadrilateral.
So, ∠BAD + ∠BCD = 180° [As sum of opposite angles in a cyclic quadrilateral = 180°]
⇒ ∠BCD = 180° - ∠BAD
= 180° - 96°
= 84°.
As DCE is a straight line.
∴ ∠BCE = 180° - ∠BCD
= 180° - 84° = 96°.
BCEF is a cyclic quadrilateral,
So, ∠BCE + ∠BFE = 180°
⇒ ∠BFE = 180° - ∠BCE
= 180° - 96°
= 84°.
Hence, ∠BCD = 84° and ∠BFE = 84°.
(ii) Now, ∠BAD + ∠BFE = 96° + 84° = 180°.
But these two are interior angles on the same side of a pair of lines AD and FE.
Hence, proved that AD || FE.
Answered By
9 Likes
Related Questions
Prove that:
(i) the parallelogram, inscribed in a circle, is a rectangle.
(ii) the rhombus, inscribed in a circle, is a square.
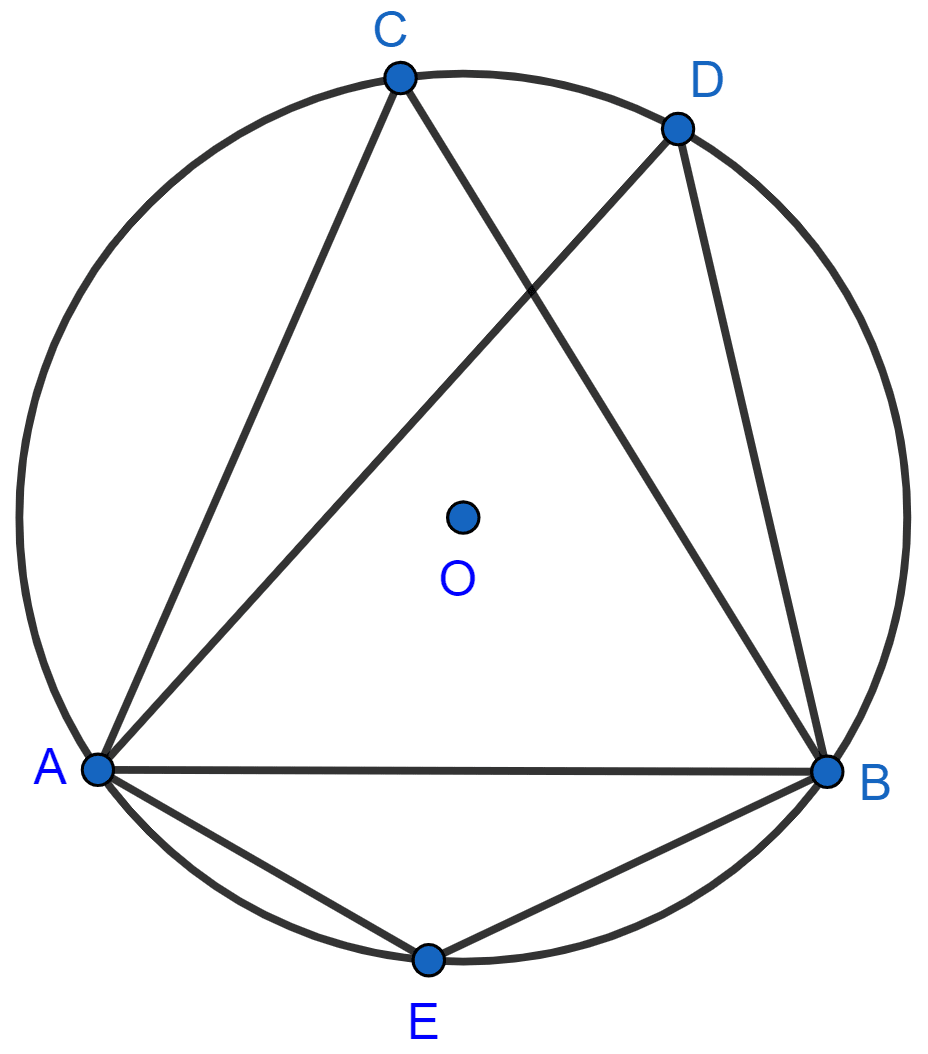
In the following figure, O is the centre of the circle and ΔABC is equilateral.
Find:
(i) ∠ADB, (ii) ∠AEB.
ABCD is a parallelogram. A circle through vertices A and B meets side BC at point P and side AD at point Q. Show that quadrilateral PCDQ is cyclic.
ABCD is a cyclic quadrilateral in a circle with centre O. If ∠ADC = 130°, find ∠BAC.
