Mathematics
In the following figure, ABCD is a parallelogram. Prove that :
(i) AP bisects angle A
(ii) BP bisects angle B
(iii) ∠DAP + ∠CBP = ∠APB
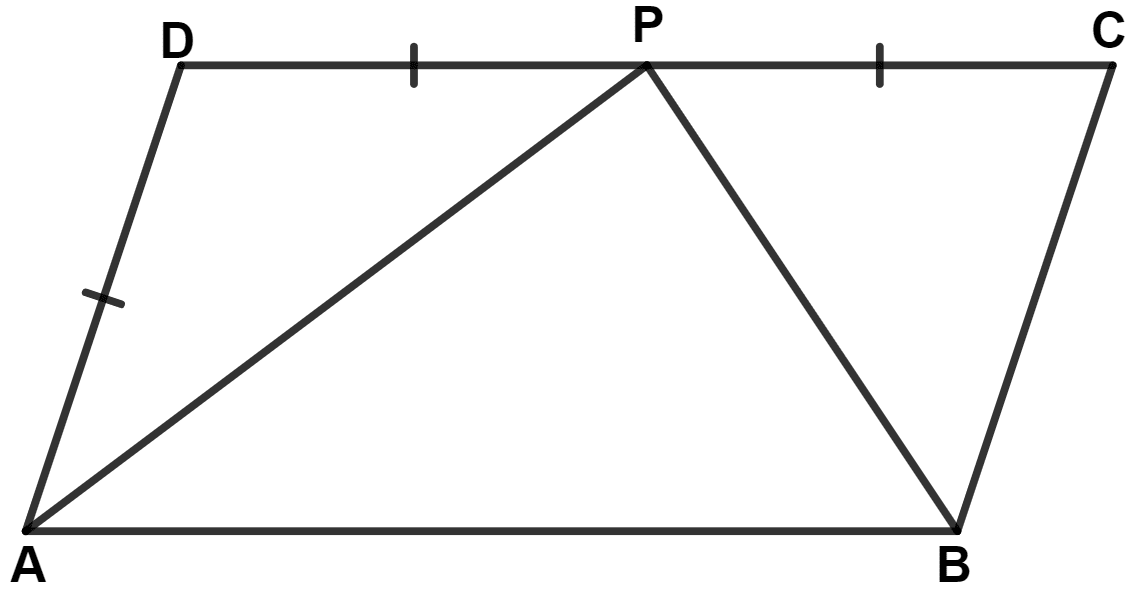
Rectilinear Figures
2 Likes
Answer
(i) In △ ADP,
⇒ AD = DP (Given)
∴ ∠APD = ∠PAD (Angles opposite to equal sides are equal) …….(1)
In parallelogram ABCD,
AB || DC and AP is the transversal.
∴ ∠APD = ∠PAB (Alternate angles are equal) ……..(2)
From equation (1) and (2), we get :
⇒ ∠PAD = ∠PAB.
∴ AP bisects angle A.
Hence, proved that AP bisects angle A.
(ii) In || gm ABCD,
⇒ BC = AD (Opposite sides of || gm are equal)
∴ BC = PC
∴ ∠BPC = ∠PBC (Angles opposite to equal sides are equal) …….(3)
In parallelogram ABCD,
AB || DC and BP is the transversal.
∴ ∠BPC = ∠PBA (Alternate angles are equal) ……..(4)
From equation (1) and (2), we get :
⇒ ∠PBC = ∠PBA.
∴ BP bisects angle B.
Hence, proved that BP bisects angle B.
(iii) We know that,
Consecutive angles of a || gm are supplementary.
∴ ∠A + ∠B = 180°,
⇒
⇒ = 90°
⇒ = 90°
⇒ ∠PAB + ∠PBA = 90° ………(1)
In △ APB,
⇒ ∠PAB + ∠PBA + ∠APB = 180°
⇒ 90° + ∠APB = 180°
⇒ ∠APB = 180° - 90°
⇒ ∠APB = 90° ……..(2)
From figure,
⇒ ∠PAB = ∠DAP (As, AP bisects ∠A)
⇒ ∠PBA = ∠CBP (As, BP bisects ∠B)
Substituting value of ∠PAB and ∠PBA in equation (1), we get :
⇒ ∠DAP + ∠CBP = 90° ………(3)
From equation (3) and (4), we get :
⇒ ∠DAP + ∠CBP = ∠APB.
Hence, proved that ∠DAP + ∠CBP = ∠APB.
Answered By
3 Likes
Related Questions
Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.
In a quadrilateral ABCD, AB = AD and CB = CD. Prove that :
(i) AC bisects angle BAD.
(ii) AC is perpendicular bisector of BD.
In parallelogram ABCD, the bisectors of angle A meets DC at P and AB = 2AD.
Prove that :
(i) BP bisects angle B.
(ii) Angle APB = 90°.
ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ; prove that AP and DQ are perpendicular to each other.