KnowledgeBoat Logo

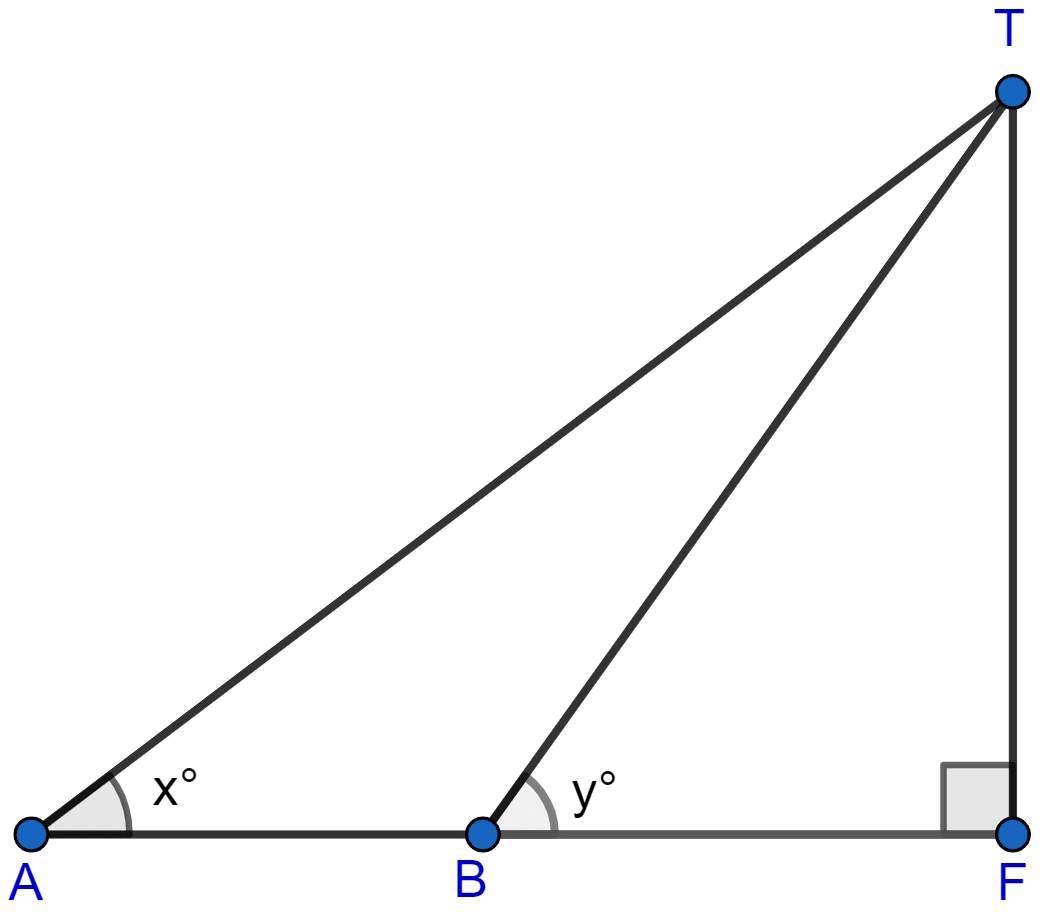
Mathematics

In the figure, not drawn to scale, TF is a tower. The elevation of T from A is x° where tan x = 25\dfrac{2}{5} and AF = 200 m. The elevation of T from B, where AB = 80 m, is y°. Calculate :

(i) the height of the tower TF.

(ii) the angle y, correct to the nearest degree.

In the figure, not drawn to scale, TF is a tower. The elevation of T from A is x° where tan x = 2/5 and AF = 200 m. The elevation of T from B, where AB = 80 m, is y°. Calculate (i) the height of the tower TF (ii) the angle y, correct to the nearest degree. Heights and Distances, ML Aggarwal Understanding Mathematics Solutions ICSE Class 10.

Heights & Distances

37 Likes

Answer

(i) From figure,

Considering right angled △AFT, we get

⇒tan x°=TFAF⇒25=TF200⇒TF=2×2005⇒TF=80\Rightarrow \text{tan x°} = \dfrac{TF}{AF} \\[1em] \Rightarrow \dfrac{2}{5} = \dfrac{TF}{200} \\[1em] \Rightarrow TF = \dfrac{2 \times 200}{5} \\[1em] \Rightarrow TF = 80

Hence, the height of the tower is 80 meters.

(ii) From figure,

BF = AF - AB = 200 - 80 = 120 meters.

Considering right angled △BFT, we get

⇒tan y°=TFBF⇒tan y°=80120⇒tan y°=0.667⇒tan y°=tan 33° 41′⇒y°=33°41′\Rightarrow \text{tan y°} = \dfrac{TF}{BF} \\[1em] \Rightarrow \text{tan y°} = \dfrac{80}{120} \\[1em] \Rightarrow \text{tan y°} = 0.667 \\[1em] \Rightarrow \text{tan y°} = \text{tan 33° 41}' \\[1em] \Rightarrow \text{y°} = 33° 41'

Rounding off to nearest degree, y = 34°.

Hence, angle y = 34°.

Answered By

21 Likes

Related Questions