Mathematics
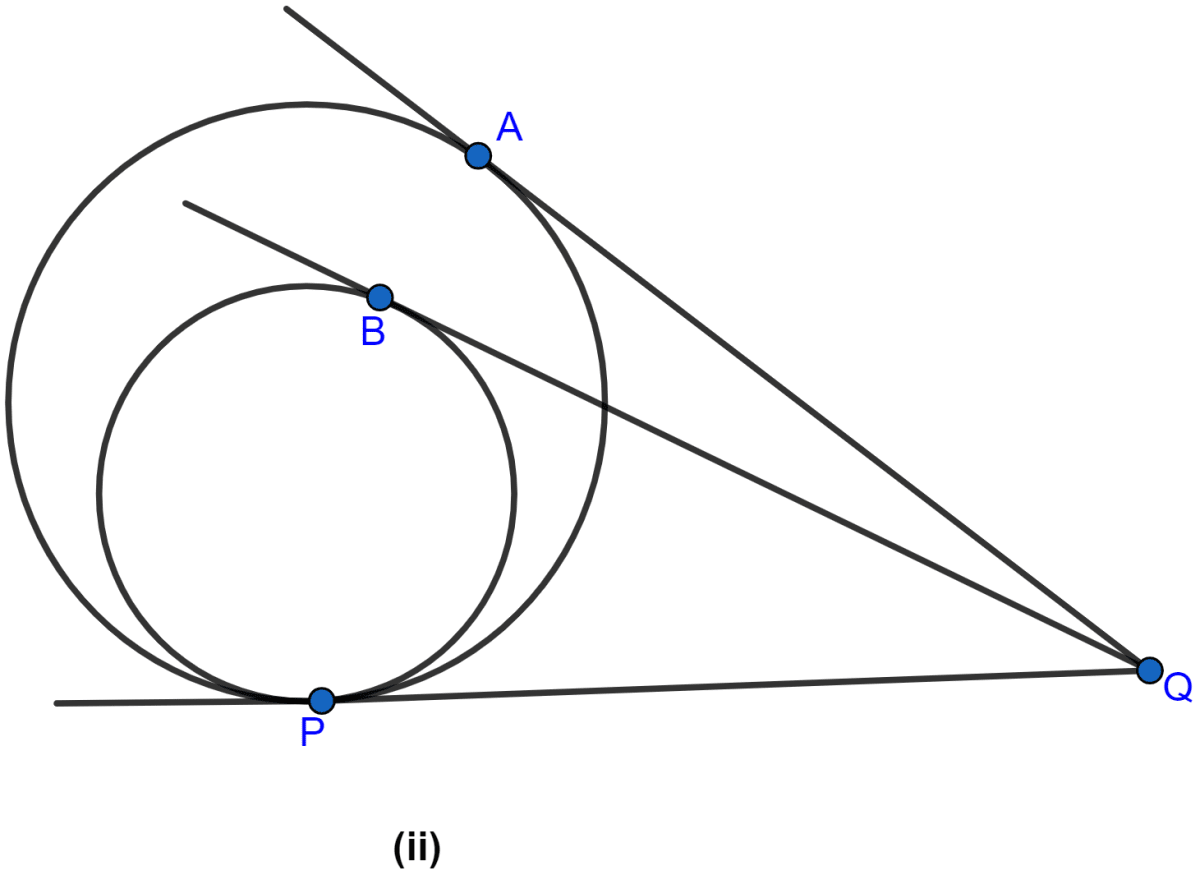
In the figure (ii) given below, two circles touch internally at P from an external point Q on the common tangent at P, two tangents QA and QB are drawn to the two circles. Prove that QA = QB.
Answer
From figure,
QA and QP are the tangents to the outer circle.
∴ QA = QP …..(i) (∵ the length of the different tangents to a circle from a single point are equal.)
Similarly, from Q, QB and QP are the tangents to the inner circle.
∴ QB = QP …..(ii) (∵ the length of the different tangents to a circle from a single point are equal.)
From (i) and (ii),
QA = QB.
Hence, proved that QA = QB.
Related Questions
Two circles with centres A, B are of radii 6 cm and 3 cm respectively. If AB = 15 cm, find the length of a transverse common tangent to these circles.
In the figure (i) given below, PA and PB are tangents at the points A and B respectively of a circle with centre O. Q and R are points on the circle If ∠APB = 70°, find
(i) ∠AOB
(ii) ∠AQB
(iii) ∠ARB

In the given figure, tangents PQ and PR are drawn from an external point P to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.

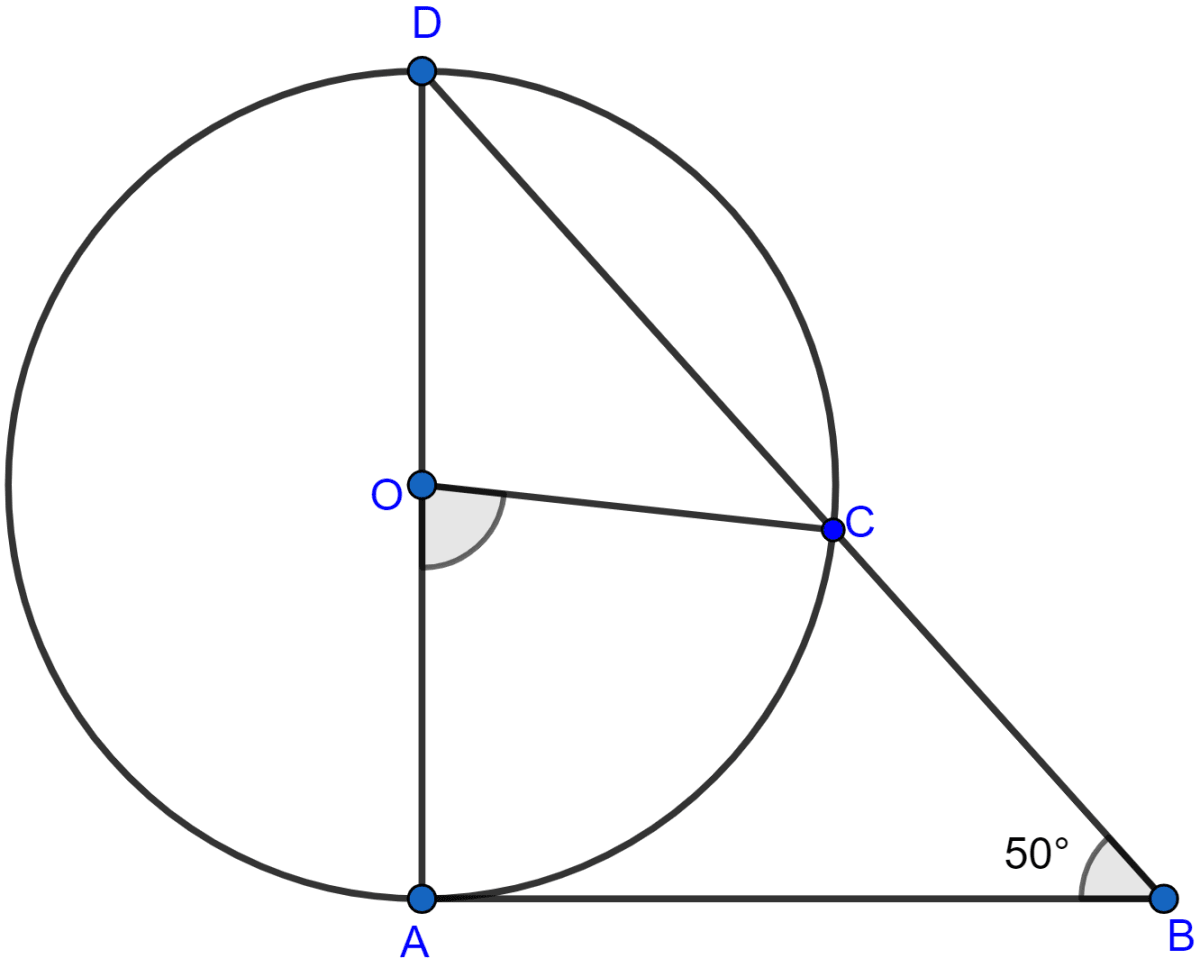
In the given figure, AD is a diameter of a circle with centre O and AB is tangent at A. C is a point on the circle such that DC produced intersects the tangent at B. If ∠ABC = 50°, find ∠AOC.