Mathematics
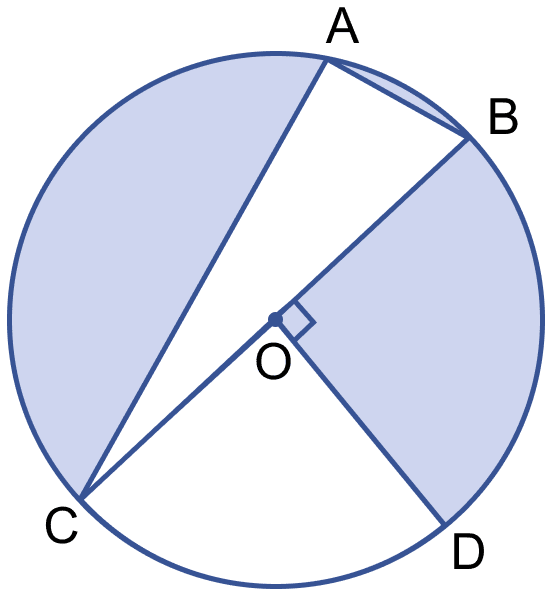
In the figure (ii) given below, O is the centre of a circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of the shaded region. (Use π = 3.14)
Mensuration
25 Likes
Answer
We know that,
Angle in semi-circle = 90°.
∴ ∠A = 90°.
In right angle △ABC
Using Pythagoras theorem,
⇒ BC2 = AC2 + AB2
⇒ BC2 = 242 + 72
⇒ BC2 = (576 + 49) = 625
⇒ BC = = 25 cm.
From figure,
Radius of circle (OB) = = 12.5 cm.
By formula,
Area of △ABC = × AB × AC
= × 7 × 24
= 84 cm2.
Area of circle = πr2
= 3.14 × 12.5 × 12.5
= 490.63 cm2.
Area of quadrant COD = = 122.66 cm2.
Area of shaded portion = Area of circle – (Area of △ABC + Area of quadrant COD)
= 490.63 – (84 + 122.66)
= 490.63 – 206.66
= 283.97 cm2.
Hence, area of shaded portion = 283.97 cm2.
Answered By
17 Likes
Related Questions
In the figure (ii) given below, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA = 20 cm, find the area of the shaded region. (π = 3.14)

In the figure (i) given below, ABCD is a rectangle, AB = 14 cm and BC = 7 cm. Taking DC, BC and AD as diameters, three semicircles are drawn as shown in the figure. Find the area of the shaded portion.
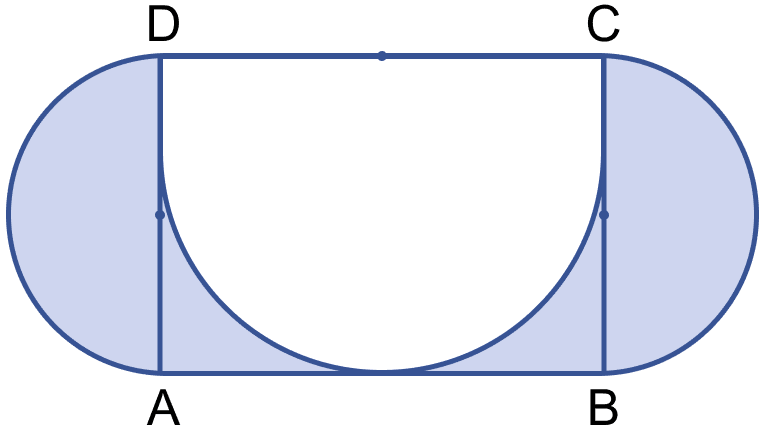
In the figure (i) given below, ABCD is a square of side 14 cm. A, B, C and D are centres of the equal circles which touch externally in pairs. Find the area of the shaded region.

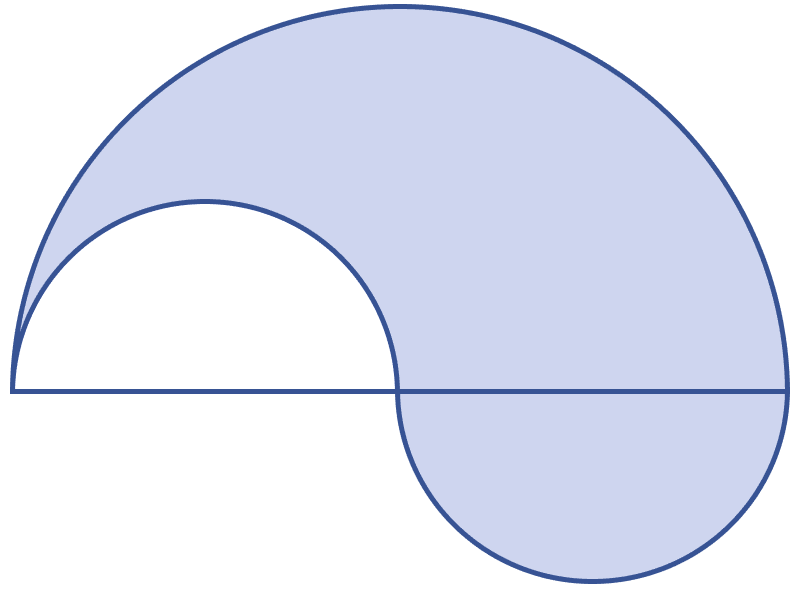
In the figure (ii) given below, the boundary of the shaded region in the given diagram consists of three semicircular arcs, the smaller being equal. If the diameter of the larger one is 10 cm, calculate.
(i) the length of the boundary.
(ii) the area of the shaded region. (Take π to be 3.14)