Mathematics
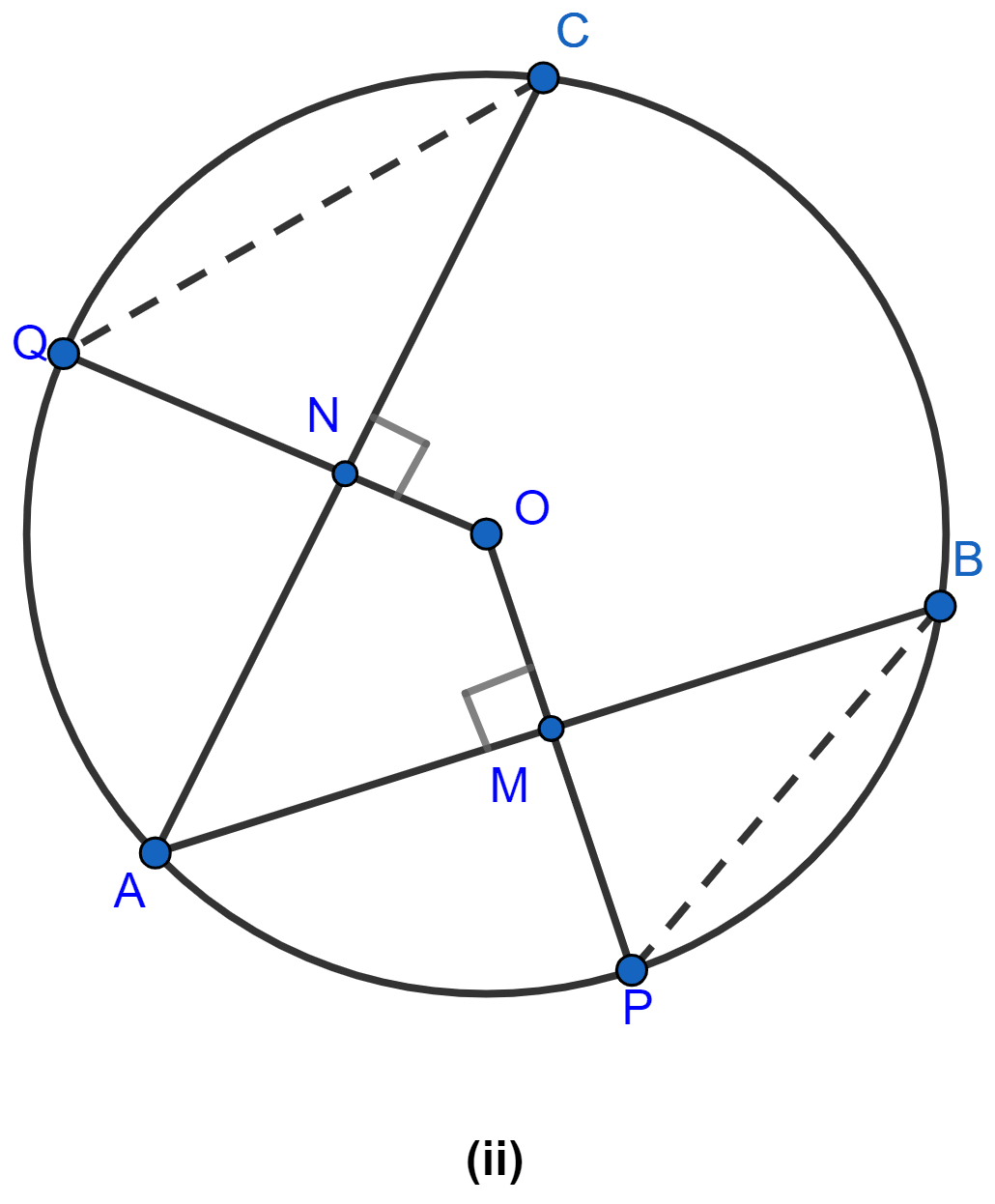
In the figure (ii) given below, chords AB and CD of a circle with centre O intersect at E. If OE bisects ∠AED, prove that AB = CD.

Answer
Draw perpendiculars from O to AB and CD.

In △OME and △ONE,
∠OME = ∠ONE = 90°
∠OEM = ∠OEN (Given) = x° (let)
In △OME,
⇒ ∠OME + ∠OEM + ∠MOE = 180°
⇒ 90° + x° + ∠MOE = 180°
⇒ ∠MOE = (90 - x)°
In △ONE,
⇒ ∠ONE + ∠OEN + ∠NOE = 180°
⇒ 90° + x° + ∠NOE = 180°
⇒ ∠NOE = (90 - x)°
∴ ∠MOE = ∠NOE
∴ △OME ≅ △ONE (By A.A.A. axiom)
∴ OM = ON (By C.P.C.T.)
Hence, chords AB and CD are equidistant from the center of circle
Since, chords of a circle that are equidistant from the centre of the circle are equal,
∴ AB = CD.
Hence, proved that AB = CD.
Related Questions
In the figure (i) given below, AD is a diameter of a circle with center O. If AB || CD, prove that AB = CD.

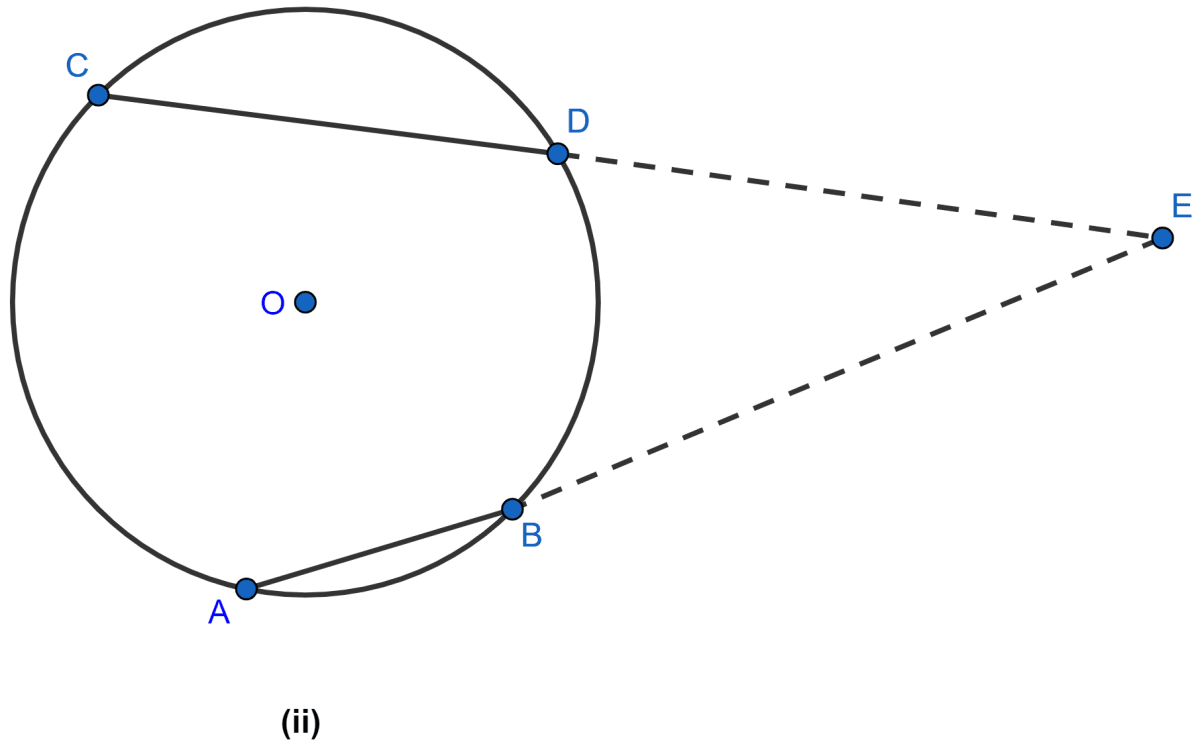
In the figure (ii) given below, AB and CD are equal chords of a circle with center O. If AB and CD meet at E (outside the circle) prove that
(i) AE = CE
(ii) BE = DE.
In the figure (ii) given below, O is the center of a circle. If AB and AC are chords of the circle such that AB = AC and OP ⊥ AB, OQ ⊥ AC, prove that PB = QC.
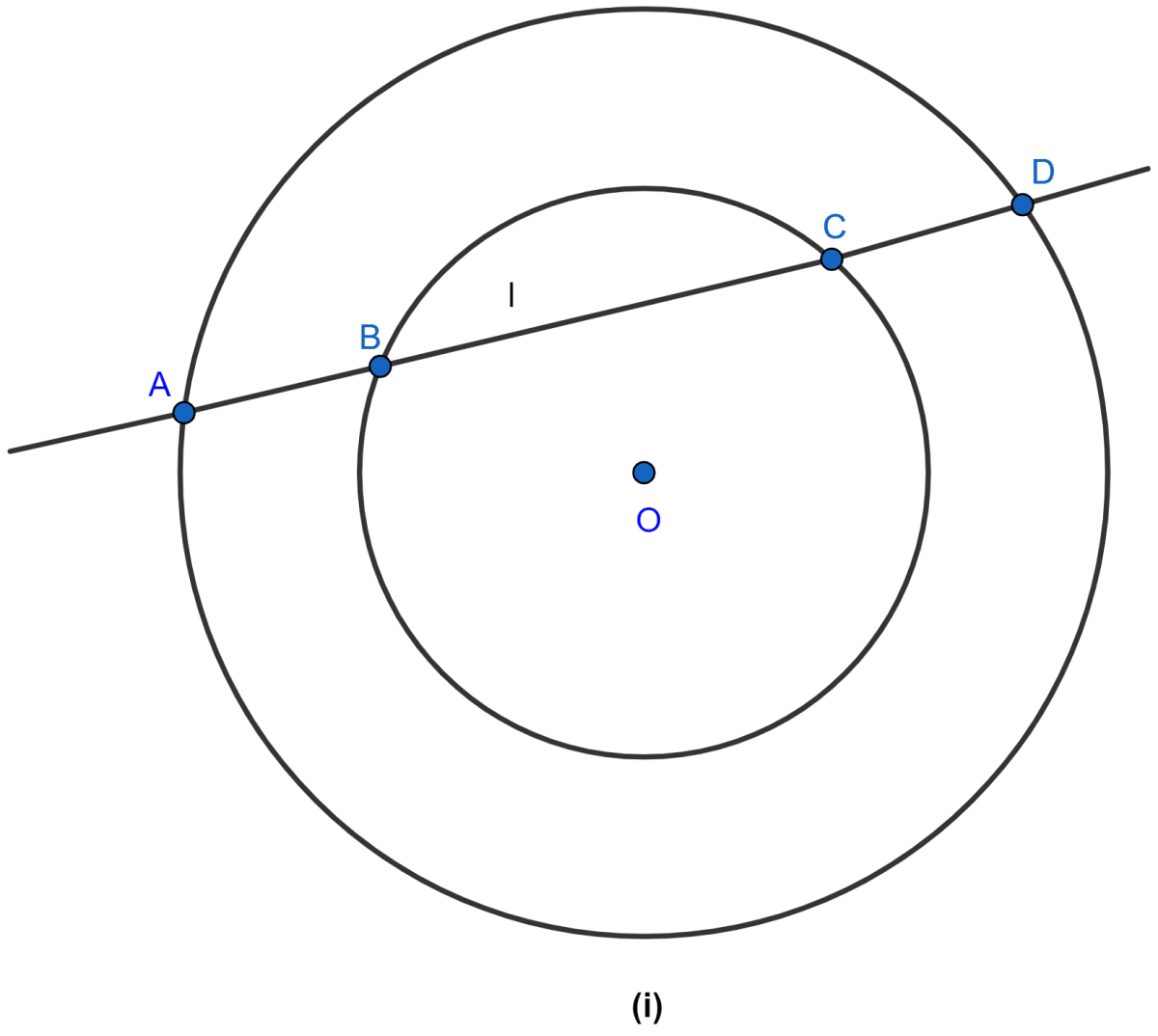
In the figure (i) given below, a line l intersects two concentric circles at the points A, B, C and D. Prove that AB = CD.