Mathematics
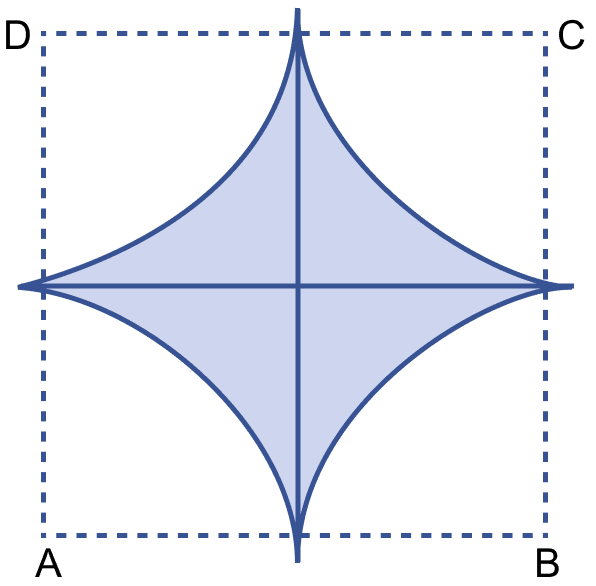
In the figure (ii) given below, ABCD is a square. Points A, B, C and D are centres of quadrants of circles of the same radius. If the area of the shaded portion is cm2, find the radius of the quadrants.
Mensuration
7 Likes
Answer
Let radius be r cm of each quadrant.
Area of each quadrant =
So, area of 4 quadrants =
From figure,
Side of square = r + r = 2r
Area of square ABCD = (Side)2 = (2r)2 = 4r2.
Area of shaded region = Area of square ABCD - Area of 4 quadrants
Hence, radius of quadrant = 5 cm.
Answered By
4 Likes
Related Questions
In the figure (i) given below, a piece of cardboard in the shape of a quadrant of a circle of radius 7 cm is bounded by the perpendicular radii OX and OY. Points A and B lie on OX and OY respectively such that OA = 3 cm and OB = 4 cm. The triangular part OAB is removed. Calculate the area and the perimeter of the remaining piece.

The length of minute hand of a clock is 14 cm. Find the area swept by the minute hand in 15 minutes.
In the adjoining figure, ABC is a right angled triangle right angled at B. Semicircles are drawn on AB, BC and CA as diameter. Show that the sum of areas of semicircles drawn on AB and BC as diameter is equal to the area of the semicircle drawn on CA as diameter.

In the figure (ii) given below, there are five squares each of side 2 cm.
(i) Find the radius of the circle.
(ii) Find the area of the shaded region. (Take π = 3.14).
