Mathematics
In the figure (i) given below, PQRS is a cyclic quadrilateral in which PQ = QR and RS is produced to T. If ∠QPR = 52°, calculate ∠PST.

Answer
Given, ∠QPR = 52°.
Since PQ = PR so, ∠QRP = ∠QPR = 52°.
Since sum of angles of triangle = 180°
In △PQR
⇒ ∠QPR + ∠QRP + ∠PQR = 180°
⇒ 52° + 52° + ∠PQR = 180°
⇒ 104° + ∠PQR = 180°
⇒ ∠PQR = 180° - 104°
⇒ ∠PQR = 76°.
∵ exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
∠PST = ∠PQR = 76°
Hence, the value of ∠PST = 76°
Related Questions
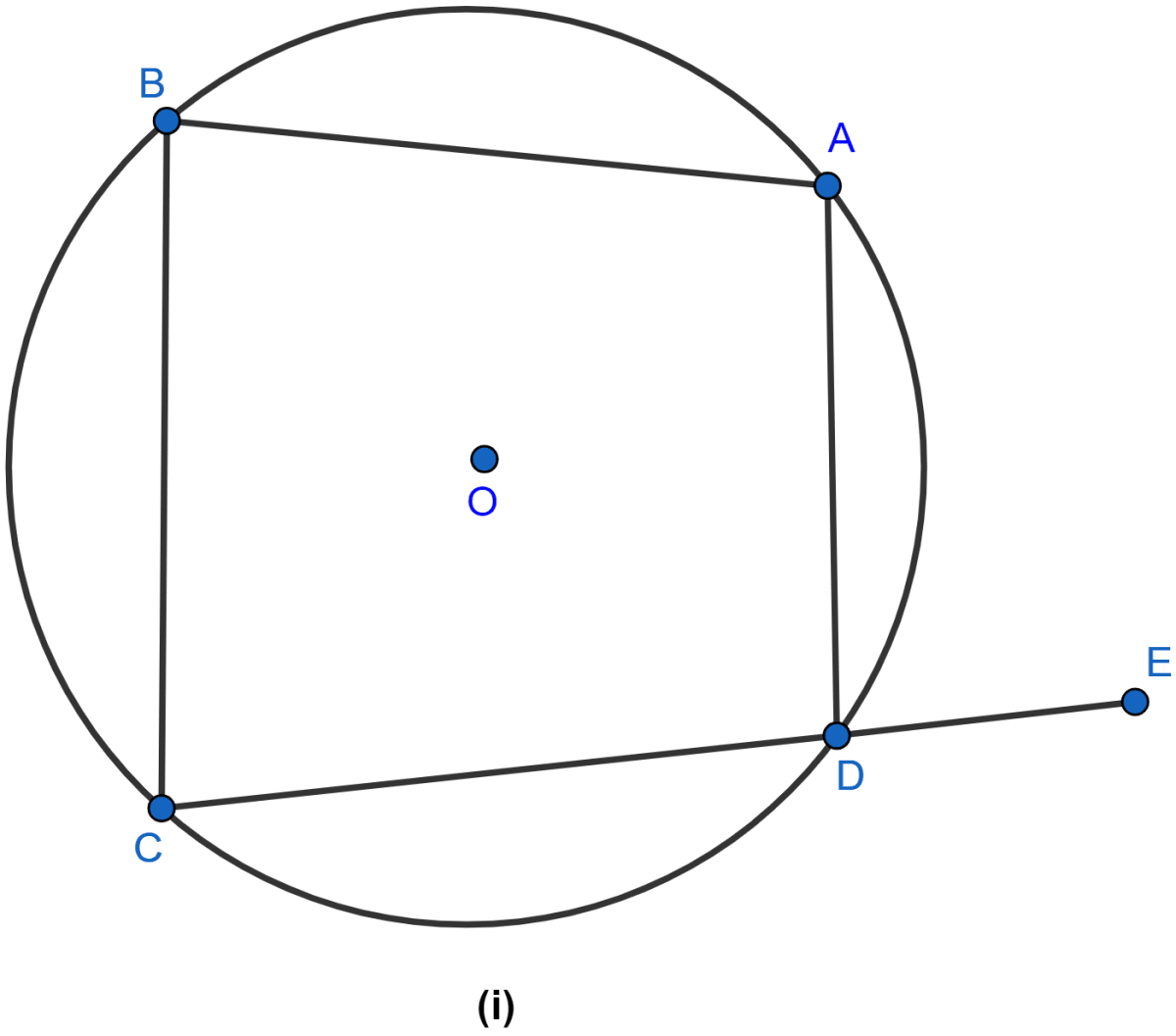
In the figure (i) given below, ABCD is a quadrilateral inscribed in a circle with centre O. CD is produced to E. If ∠ADE = 70° and ∠OBA = 45°, calculate
(i) ∠OCA
(ii) ∠BAC
In the figure (ii) given below, O is the center of the circle. If ∠OAD = 50°, find the values of x and y.

In the figure (i) given below, O is the center of the circle. If ∠COD = 40° and ∠CBE = 100°, then find :
(i) ∠ADC
(ii) ∠DAC
(iii) ∠ODA
(iv) ∠OCA

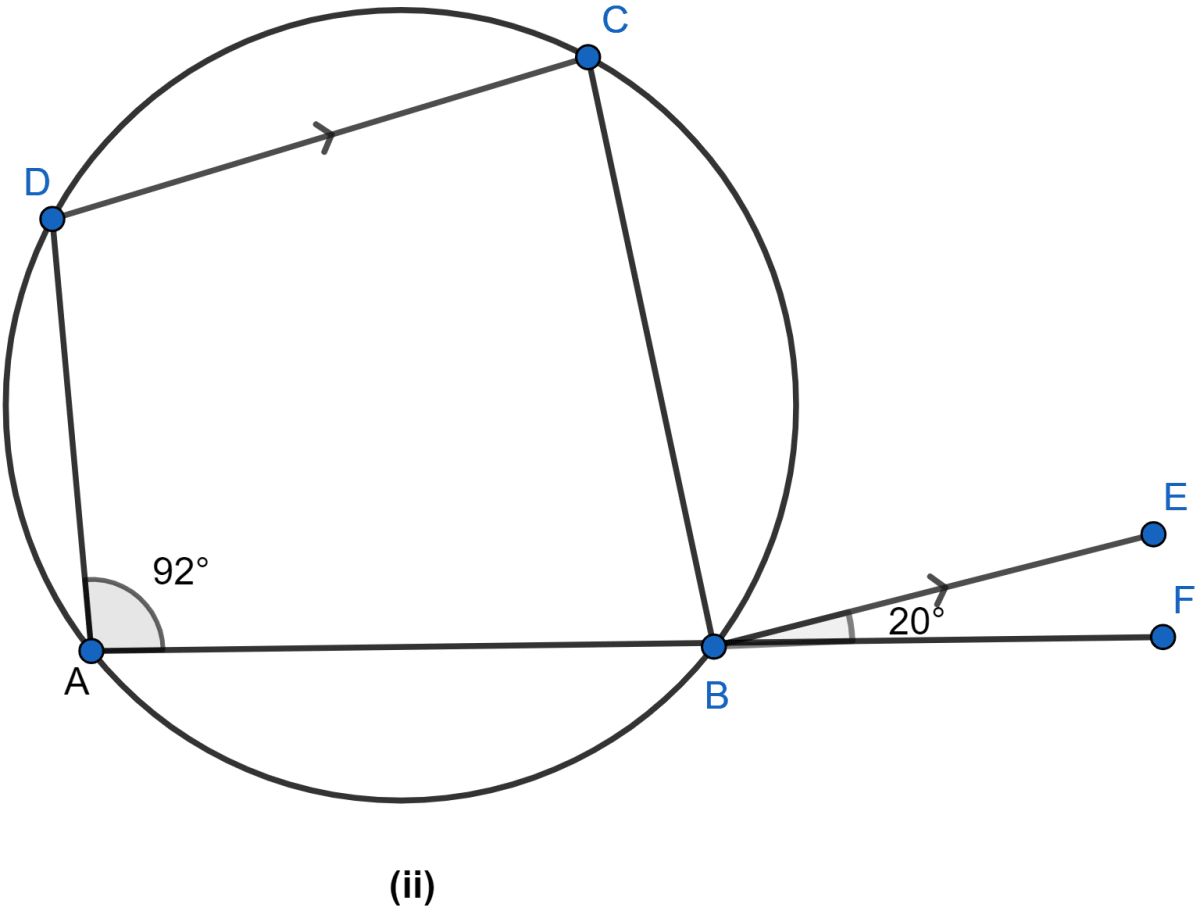
In figure (ii) given below, ABF is a straight line and BE || DC. If ∠DAB = 92° and ∠EBF = 20°, find
(i) ∠BCD
(ii) ∠ADC