Mathematics
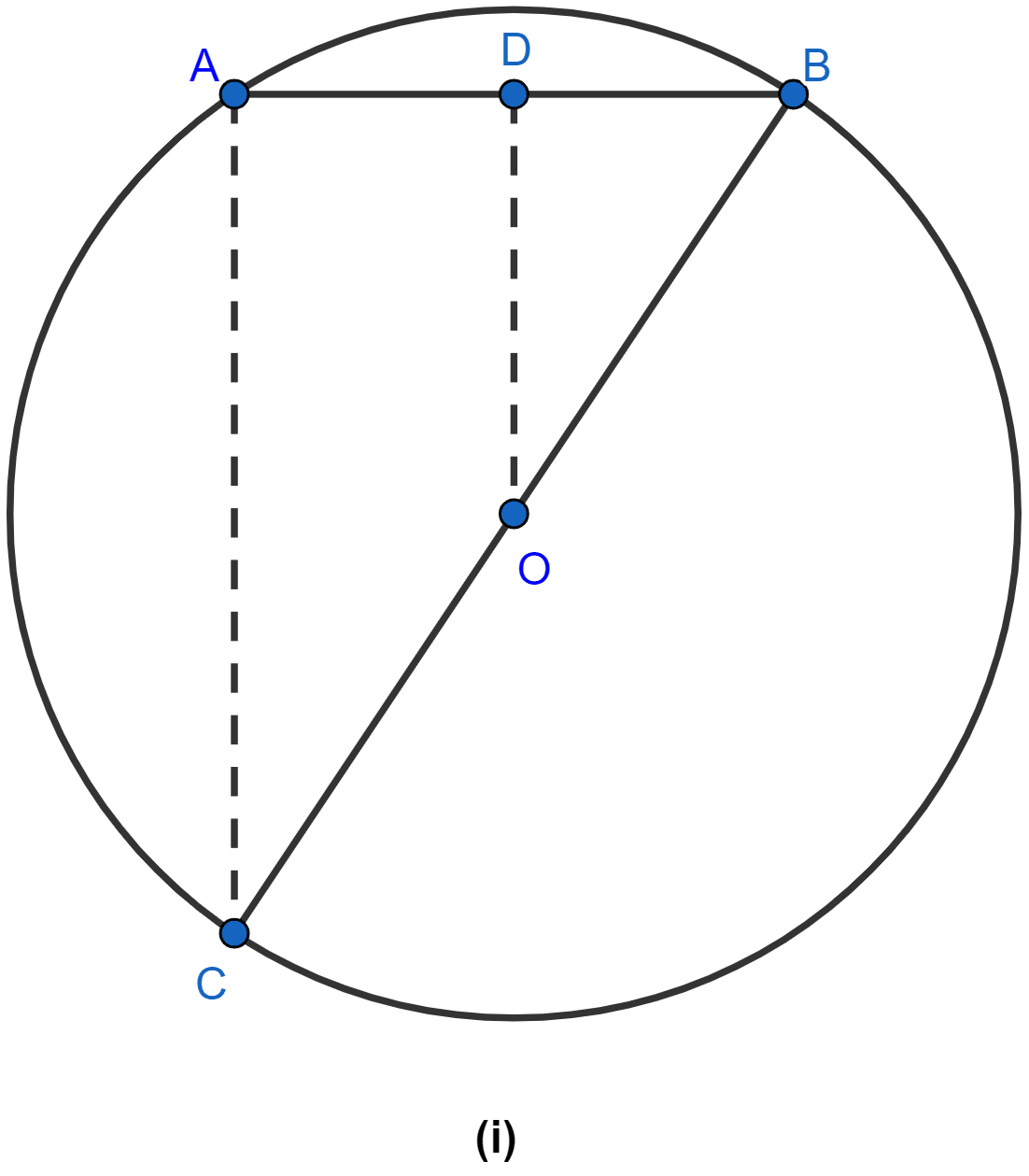
In the figure (i) given below, OD is perpendicular to the chord AB of a circle whose center is O. If BC is a diameter, show that CA = 2OD.
Circles
Answer
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ AD = DB
We can say that D is mid-point of AB.
Since, BC is diameter and O is center so, OB = OC = radius.
We can say that O is mid-point of BC.
In △ABC,
Since, D is mid-point of AB and O is mid-point of BC
By mid-point theorem,
⇒ OD || AC and OD =
⇒ AC = 2OD.
Hence, proved that CA = 2OD.
Answered By
Related Questions
If a diameter of a circle is perpendicular to one of two parallel chords of the circle, prove that it is perpendicular to the other and bisects it.
In an equilateral triangle, prove that the centroid and the circumcentre of the triangle coincide.
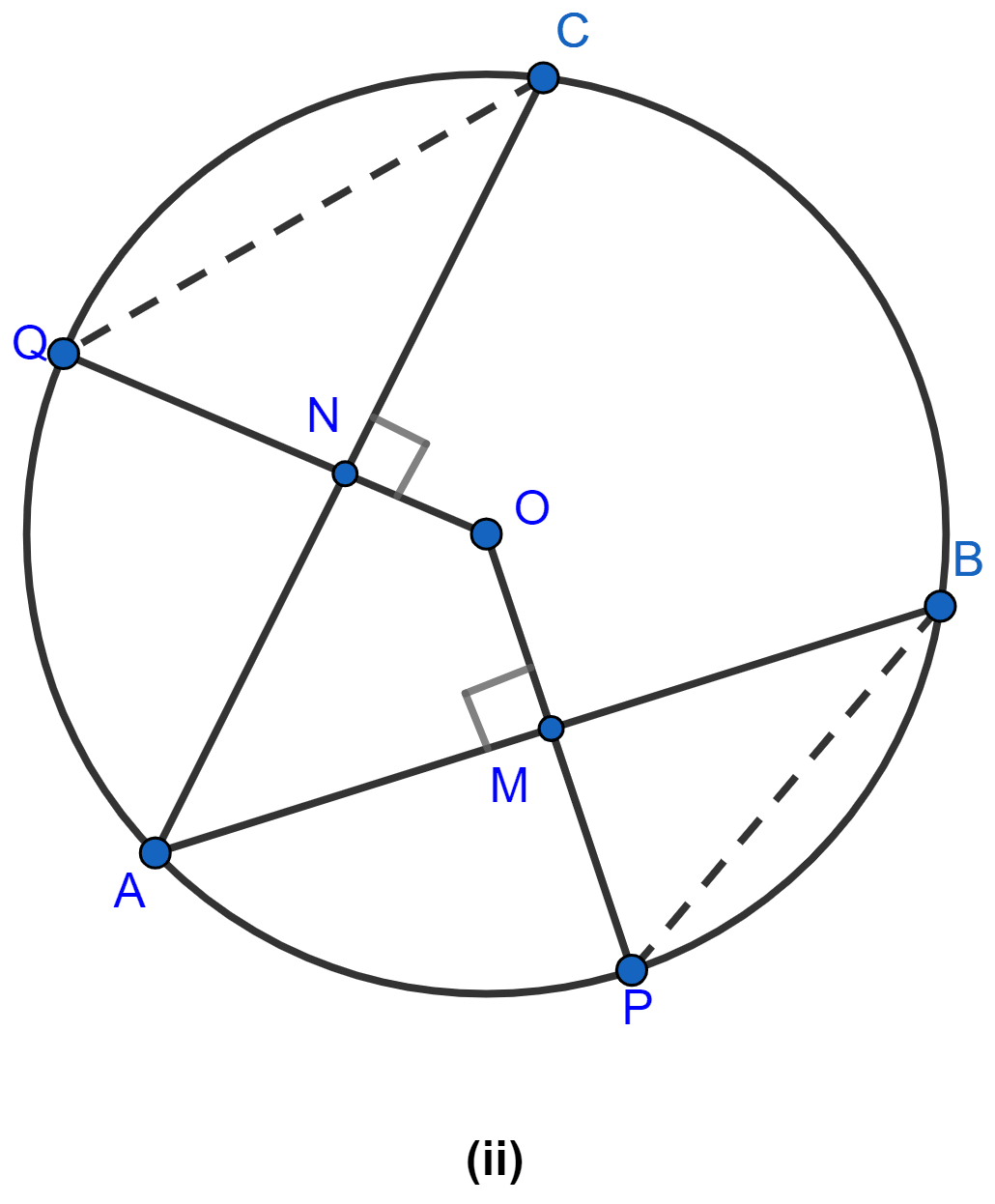
In the figure (ii) given below, O is the center of a circle. If AB and AC are chords of the circle such that AB = AC and OP ⊥ AB, OQ ⊥ AC, prove that PB = QC.
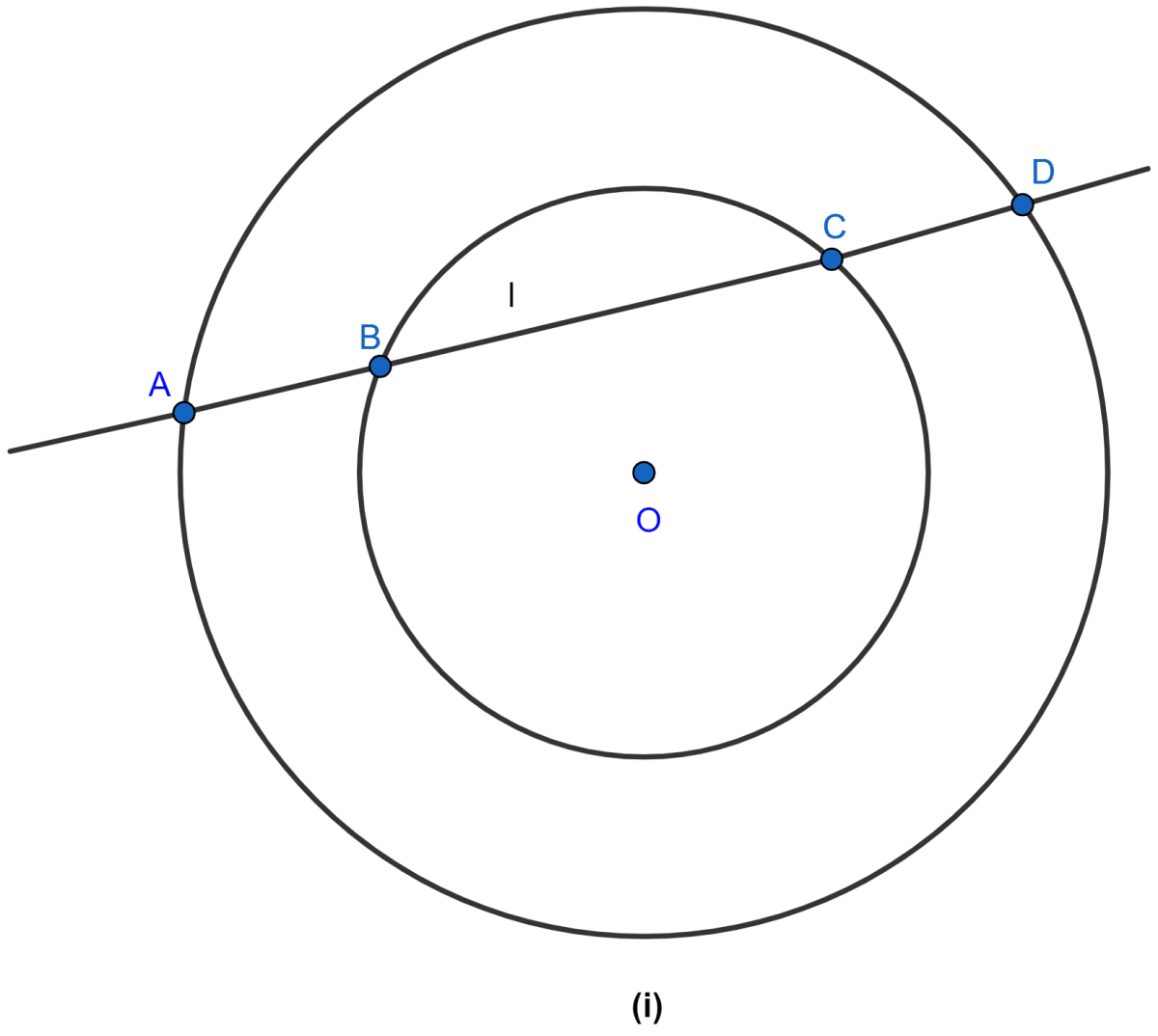
In the figure (i) given below, a line l intersects two concentric circles at the points A, B, C and D. Prove that AB = CD.