Mathematics
In the figure (i) given below, if ∠DBC = 58° and BD is a diameter of the circle, calculate
(i) ∠BDC
(ii) ∠BEC
(iii) ∠BAC

Circles
19 Likes
Answer
(i) Given,
∠DBC = 58°
From figure,
∠BCD = 90° (∵ angle in semicircle is equal to 90°.)
Since sum of angles in triangle is 180°.
∴ In △BCD
⇒ ∠DBC + ∠BCD + ∠BDC = 180°
⇒ 58° + 90° + ∠BDC = 180°
⇒ 148° + ∠BDC = 180°
⇒ ∠BDC = 180° - 148°
⇒ ∠BDC = 32°.
Hence, the value of ∠BDC = 32°.
(ii) Considering quadrilateral BDCE.
From figure,
BDCE is a cyclic quadrilateral.
Since opposite angles sum is 180° in cyclic quadrilateral
⇒ ∠BDC + ∠BEC = 180°
⇒ 32° + ∠BEC = 180°
⇒ ∠BEC = 180° - 32°
⇒ ∠BEC = 148°.
Hence, the value of ∠BEC = 148°.
(iii) From figure,
∠BAC = ∠BDC (∵ angles in same segment are equal.)
∴ ∠BAC = 32°.
Hence, the value of ∠BAC = 32°.
Answered By
10 Likes
Related Questions
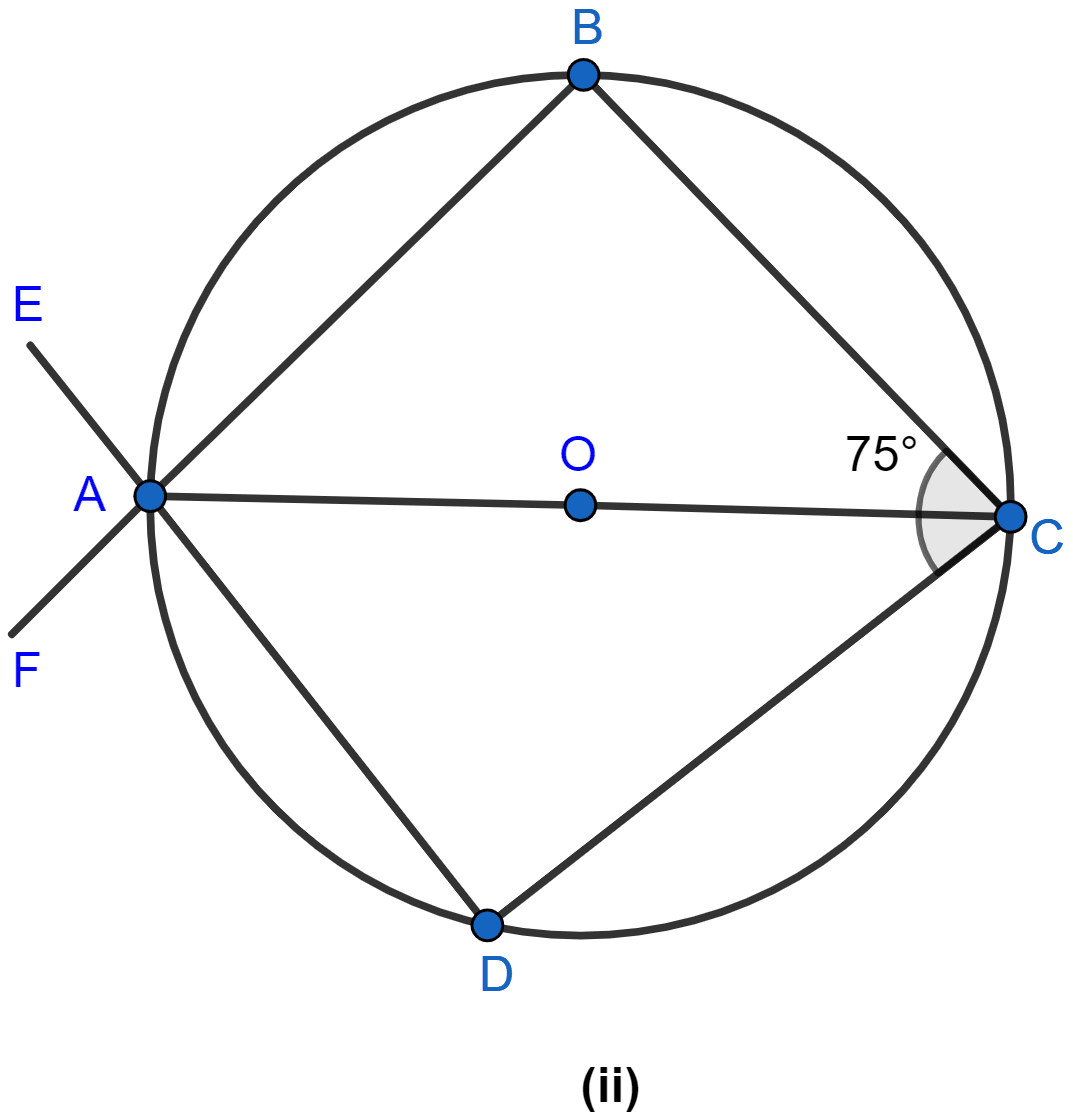
In the figure (ii) given below, AC is a diameter of the given circle and ∠BCD = 75°. Calculate the size of
(i) ∠ABC
(ii) ∠EAF
In the figure (i) given below, ABCD is a cyclic quadrilateral. If ∠ADC = 80° and ∠ACD = 52°, find the values of ∠ABC and ∠CBD.

In the figure (i) given below, O is the center of the circle. If ∠AOC = 150°, find
(i) ∠ABC
(ii) ∠ADC.

In the figure (ii) given below, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°. Find :
(i) ∠CAD
(ii) ∠CBD
(iii) ∠ADC
