Mathematics
In the figure (i) given below, chords AB and CD of a circle intersect at E.
(i) Prove that triangles ADE and CBE are similar.
(ii) Given DC = 12 cm, DE = 4 cm and AE = 16 cm, calculate the length of BE.

Circles
37 Likes
Answer
(i) In △CBE and △ADE,
∠B = ∠D (∵ angles in same segment are equal.)
∠BEC = ∠DEA (∵ vertically opposite angles are equal.)
△CBE ~ △ADE. (By AA axiom)
Hence, proved that △CBE ~ △ADE.
(ii) Given, DC = 12 cm.
From figure,
⇒ DC = DE + EC
⇒ 12 = 4 + EC
⇒ EC = 12 - 4
⇒ EC = 8 cm.
Chords AB and CD intersect each other at E.
Considering △BEC and △AED,
∠BEC = ∠DEA (∵ vertically opposite angles are equal.)
∠CBE = ∠EDA (∵ both angles are subtended on circle by arc AC and angles in same segment are equal.)
Hence, △BEC ~ △AED.
Since triangles are similar hence the ratio of the corresponding sides are equal.
Hence, the length of BE = 2 cm.
Answered By
19 Likes
Related Questions
In the figure (i) given below, CP bisects ∠ACB. Prove that DP bisects ∠ADB.

In the figure (ii) given below, BD bisects ∠ABC. Prove that .
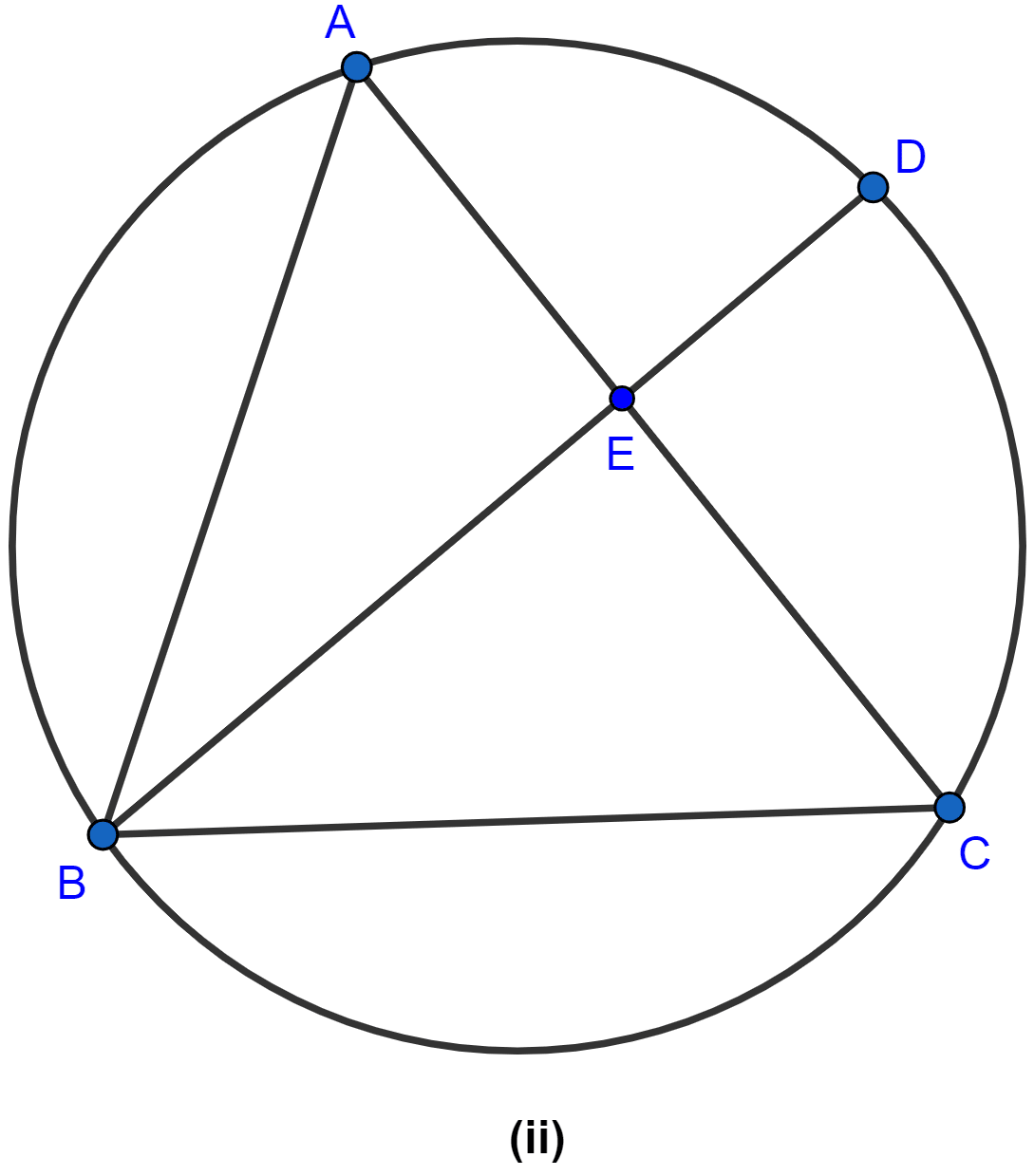
In the figure (ii) given below, AB and CD are two intersecting chords of a circle. Name two triangles which are similar. Hence, calculate CP given that AP = 6 cm, PB = 4 cm, and CD = 14 cm (PC > PD).
In the adjoining figure, AE and BC intersect each other at point D. If ∠CDE = 90°, AB = 5 cm, BD = 4 cm and CD = 9 cm, find DE.