Mathematics
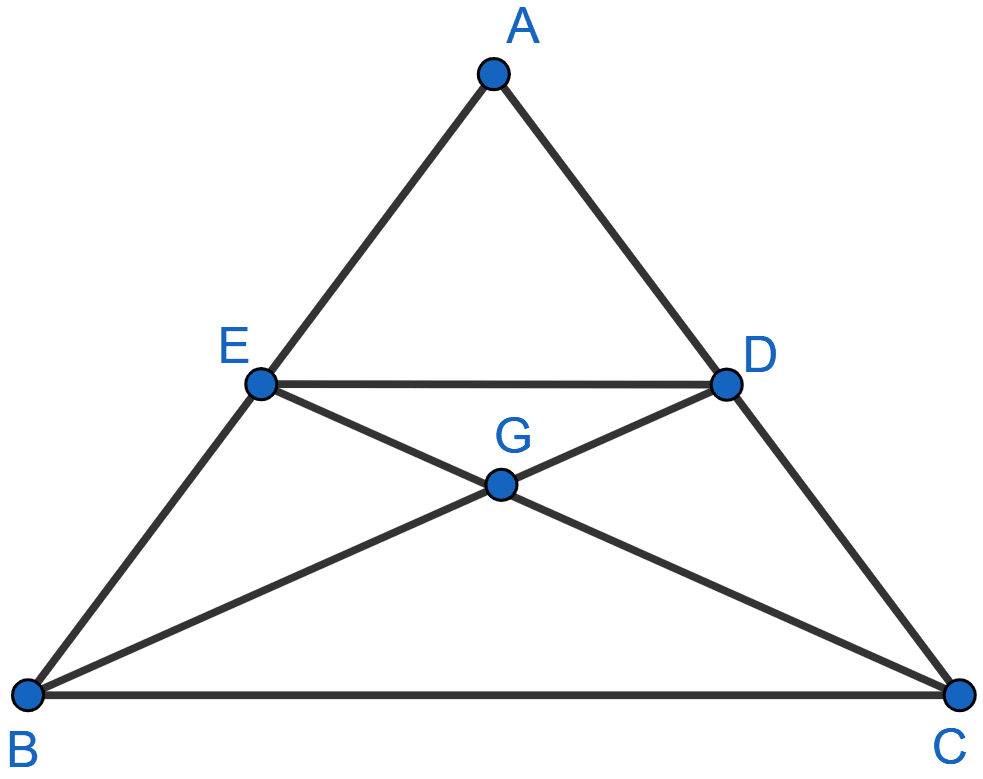
In the figure, given below, the medians BD and CE of a triangle ABC meet at G. Prove that :
(i) △EGD ~ △CGB and
(ii) BG = 2GD from (i) above.
Similarity
24 Likes
Answer
(i) Since, BD and CE are medians.
So, E is mid-point of AB and D is mid-point of AC.
By converse of mid-point theorem,
ED || BC and ED = BC
…..(1)
In △EGD and △CGB,
∠EGD = ∠BGC (Vertically opposite angles are equal)
∠DEG = ∠GCB (Alternate angles are equal)
∴ △EGD ~ △CGB [By AA].
Hence, proved that △EGD ~ △CGB.
(ii) Since, corresponding sides of similar triangle are proportional to each other.
Hence, proved that BG = 2GD.
Answered By
14 Likes
Related Questions
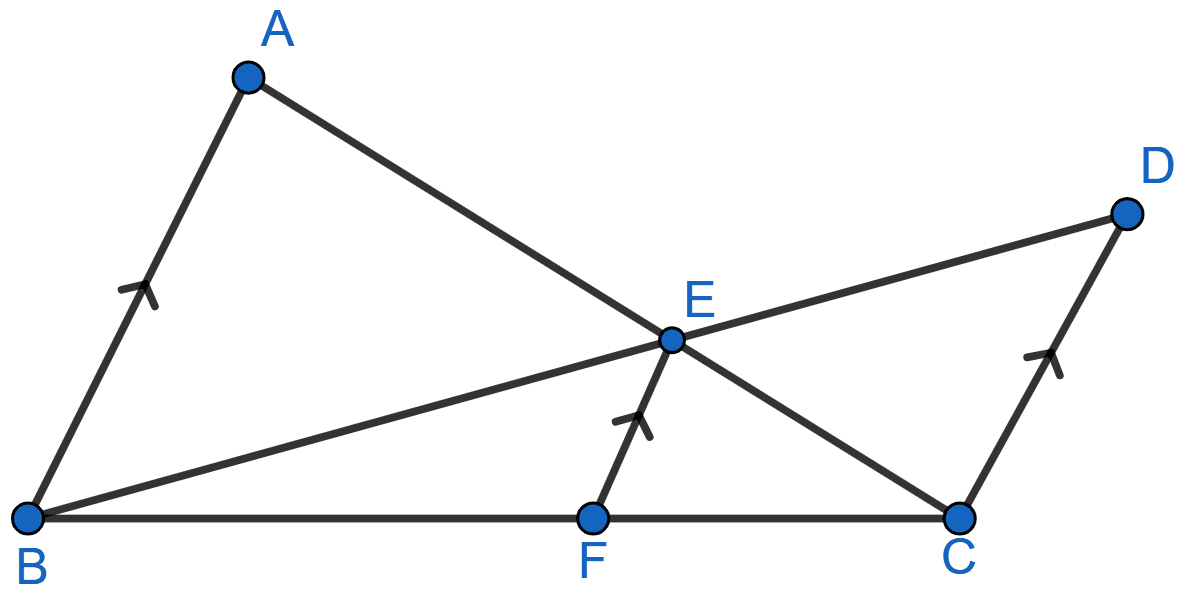
In the given figure, AB || EF || DC; AB = 67.5 cm, DC = 40.5 cm and AE = 52.5 cm.
(i) Name the three pairs of similar triangles.
(ii) Find the length of EC and EF.
In the given figure, P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC.
(i) Calculate the ratio PQ : AC, giving reason for your answer.
(ii) In triangle ARC, ∠ARC = 90° and in triangle PQS, ∠PSQ = 90°. Given QS = 6 cm, calculate the length of AR.

In the given figure, DE is parallel to BC. If AD : BD = 3 : 5 then DE : BC is :
3 : 8
3 : 5
5 : 3
8 : 3

If AD = AE and BD = CE then :
△ ADE ~ △ ACB
△ ABC ~ △ ACB
△ ABD ~ △ ABC
△ ADE ~ △ ABC
