Mathematics
In the figure given alongside, AB || CD and O is the center of the circle. If ∠ADC = 25°; find the angle AEB. Give reasons in support of your answer.

Circles
32 Likes
Answer
Join AC, BD and CB.

As angle is a semicircle is a right angle.
∴ ∠CAD = 90° and ∠CBD = 90°
Given, AB || CD
So, ∠BAD = ∠ADC = 25° [Alternate angles are equal]
From figure,
∠BAC = ∠BAD + ∠CAD = 25° + 90° = 115°.
Sum of opposite angles in a cyclic quadrilateral = 180°.
In quadrilateral ACDB,
⇒ ∠CDB + ∠BAC = 180°
⇒ ∠CDA + ∠ADB + ∠BAC = 180°
⇒ 25° + ∠ADB + 115° = 180°
⇒ ∠ADB = 180° - 115° - 25° = 40°.
As angles in same segment are equal.
∴ ∠AEB = ∠ADB = 40°.
Hence, ∠AEB = 40°.
Answered By
22 Likes
Related Questions
In cyclic quadrilateral ABCD, ∠DAC = 27°; ∠DBA = 50° and ∠ADB = 33°. Calculate :
(i) ∠DBC,
(ii) ∠DCB,
(iii) ∠CAB.

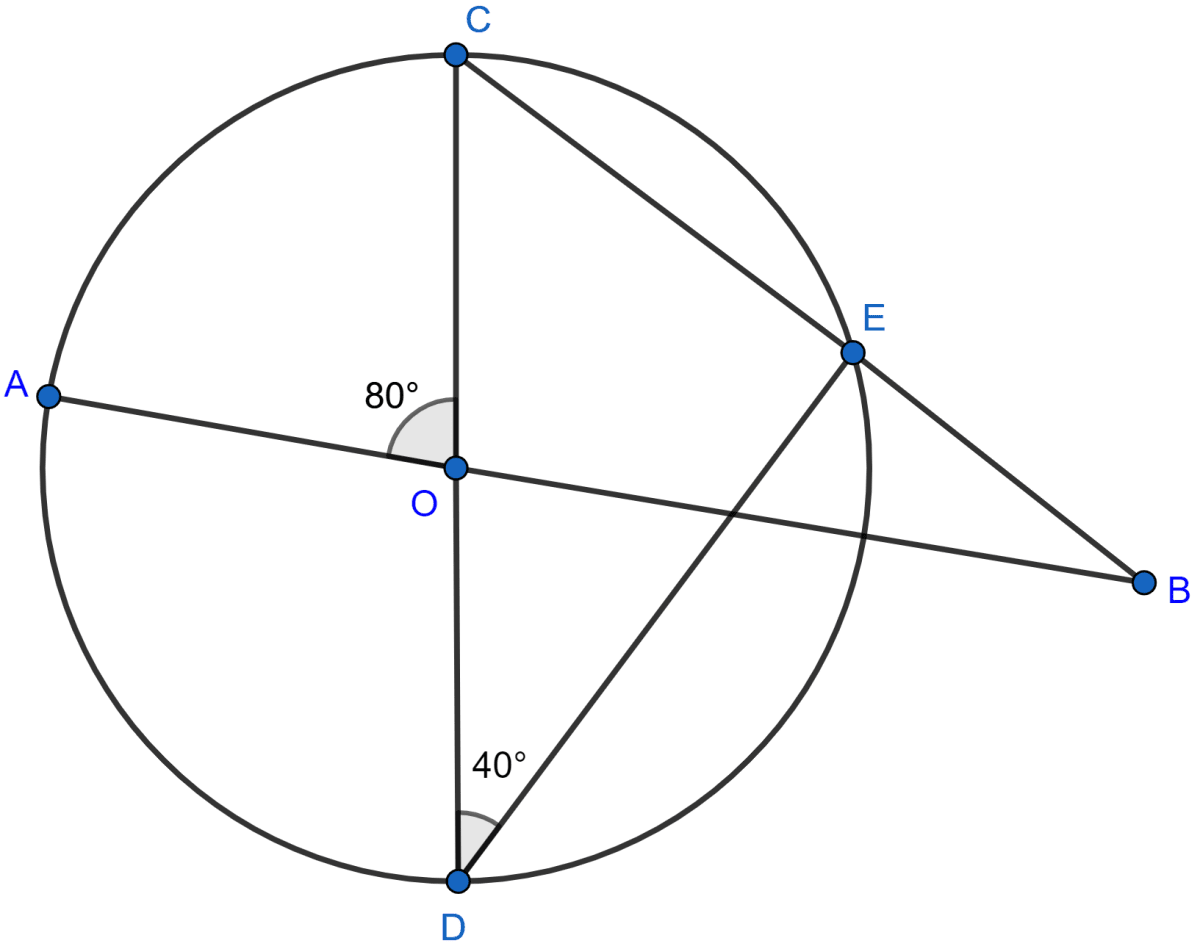
In the figure given alongside, AB and CD are straight lines through the centre O of a circle. If ∠AOC = 80° and ∠CDE = 40°, find the number of degrees in :
(i) ∠DCE,
(ii) ∠ABC.
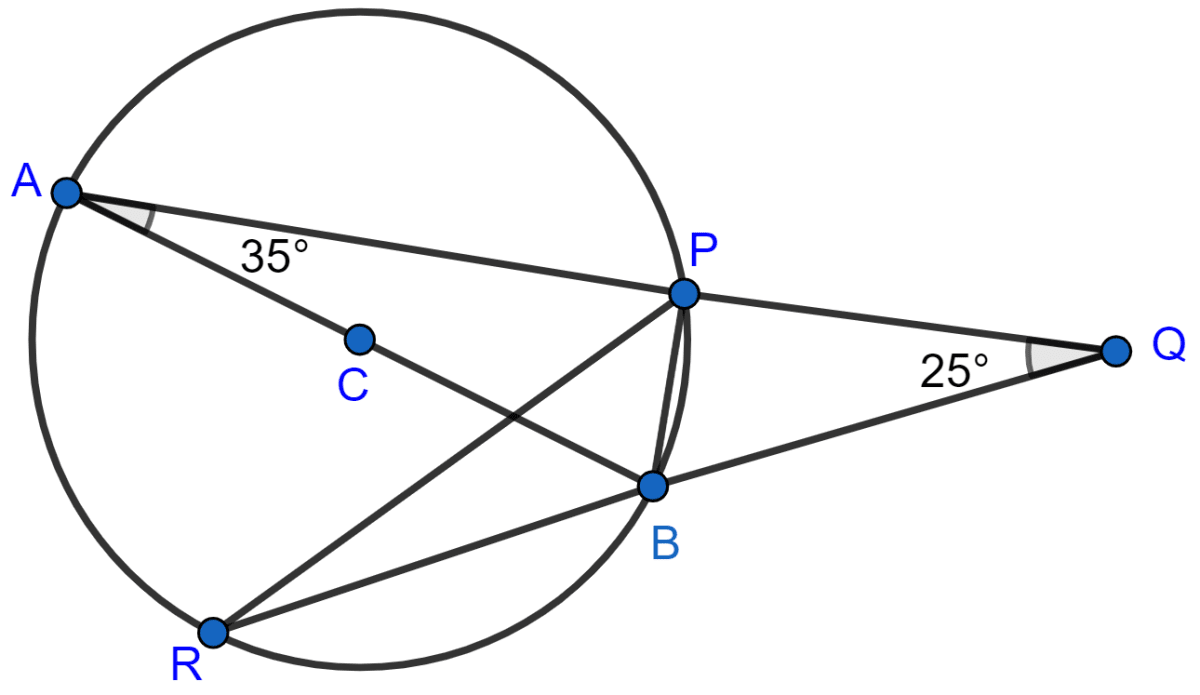
AB is a diameter of the circle APBR as shown in the figure. APQ and RBQ are straight lines. Find :
(i) ∠PRB,
(ii) ∠PBR,
(iii) ∠BPR.
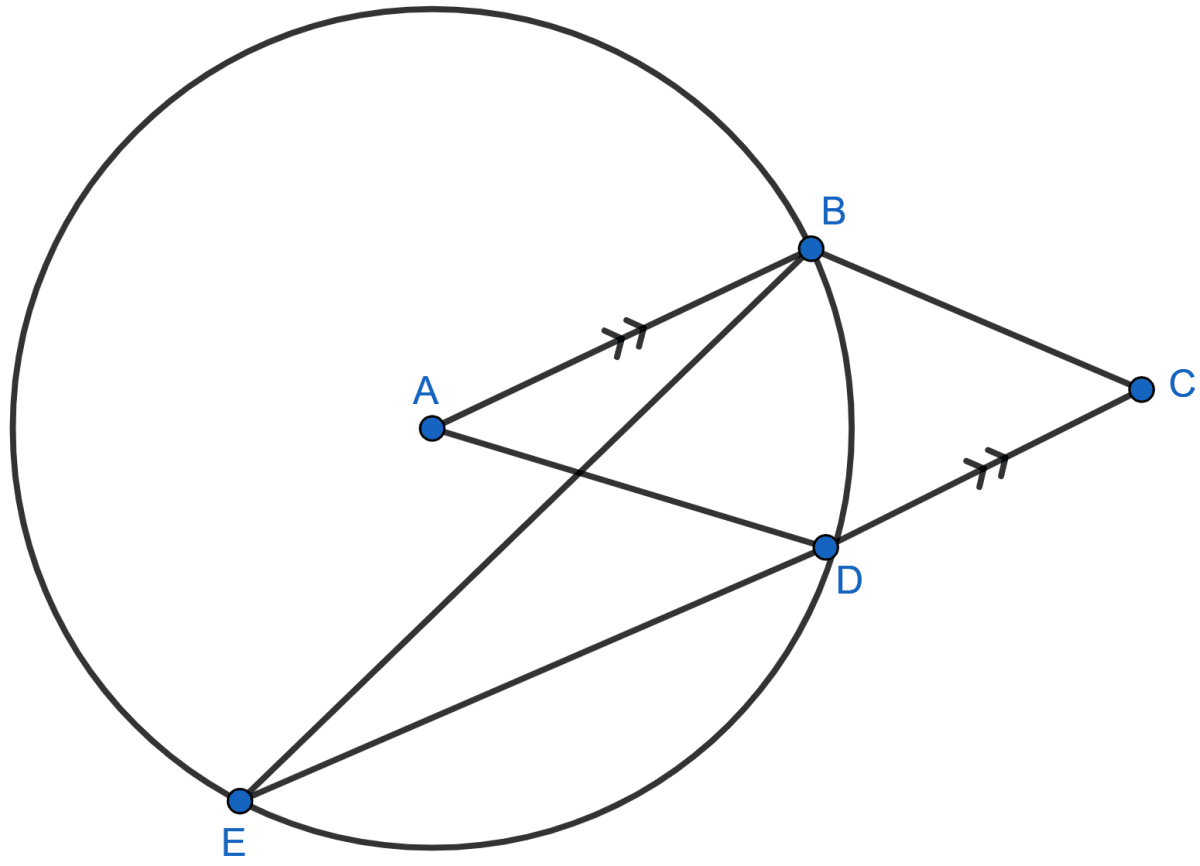
In the given figure, A is the center of the circle, ABCD is a parallelogram and CDE is a straight line. Prove that : ∠BCD = 2∠ABE.