Mathematics
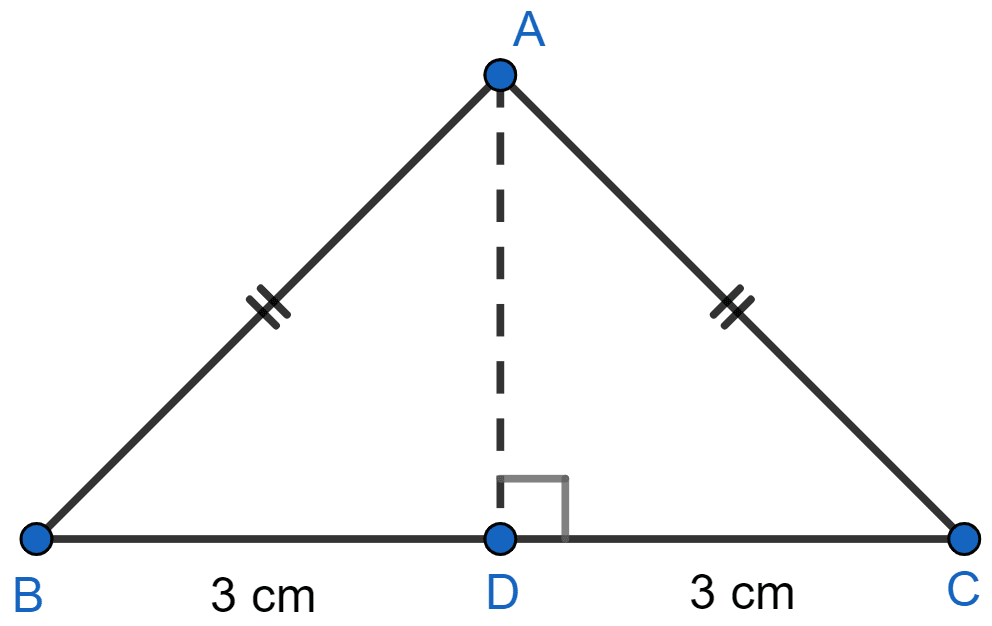
In the figure (1) given below, ∆ABC is isosceles with AB = AC = 5 cm and BC = 6 cm. Find
(i) sin C
(ii) tan B
(iii) tan C - cot B.

Trigonometrical Ratios
41 Likes
Answer
Draw AD perpendicular to BC.
D is the mid point of BC [∵ Perpendicular drawn to the unequal side of an isosceles triangle from the apex vertex bisects the side]
So, BD = CD = 3 cm.
In right-angled ∆ABD,
Using pythagoras theorem we get :
⇒ AB2 = AD2 + BD2
⇒ AD2 = AB2 - BD2
⇒ AD2 = 52 - 32
⇒ AD2 = 25 - 9
⇒ AD2 = 16
⇒ AD =
⇒ AD = 4 cm.
(i) In right-angled ∆ACD,
sin C =
= .
Hence, sin C = .
(ii) In right-angled ∆ABD,
tan B =
= .
Hence, tan B = .
(iii) In right-angled ∆ACD,
tan C =
= .
In right-angled ∆ABD,
cot B =
= .
Substituting values in tan C - cot B we get :
Hence, tan C - cot B = .
Answered By
21 Likes
Related Questions
In △PQR, ∠Q = 90°. If PQ = 40 cm and PR + QR = 50 cm, find :
(i) sin P
(ii) cos P
(iii) tan R
In △ABC, AB = AC = 15 cm, BC = 18 cm. Find
(i) cos ∠ABC
(ii) sin ∠ACB.
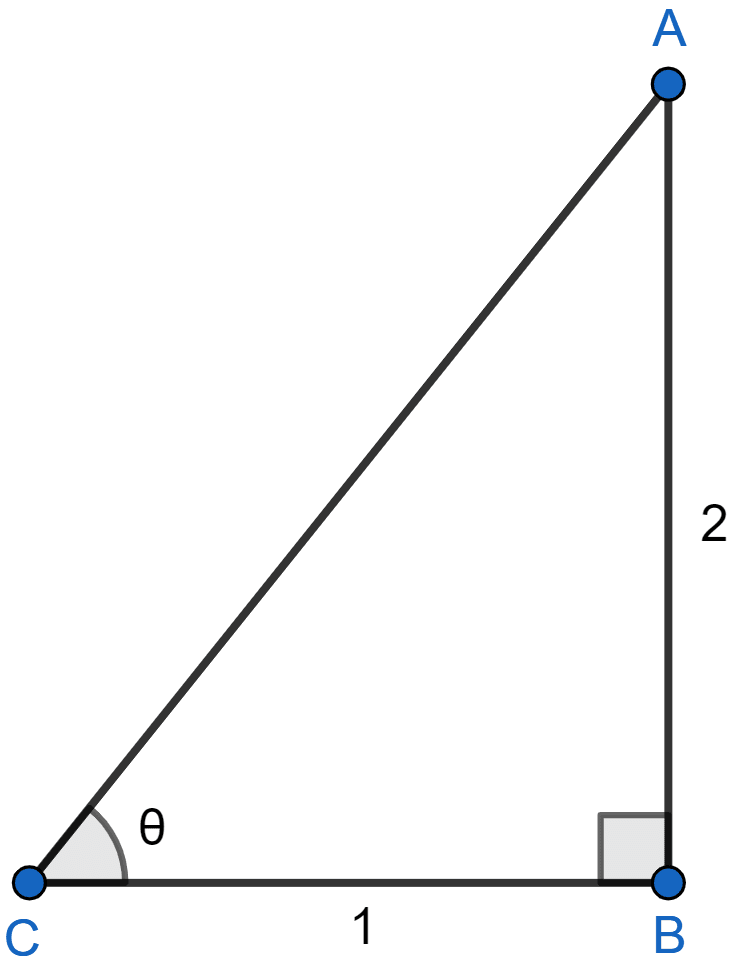
In the figure (2) given below, △ABC is right-angled at B. Given that ∠ACB = θ, side AB = 2 units and side BC = 1 unit, find the value of sin2 θ + tan2 θ.
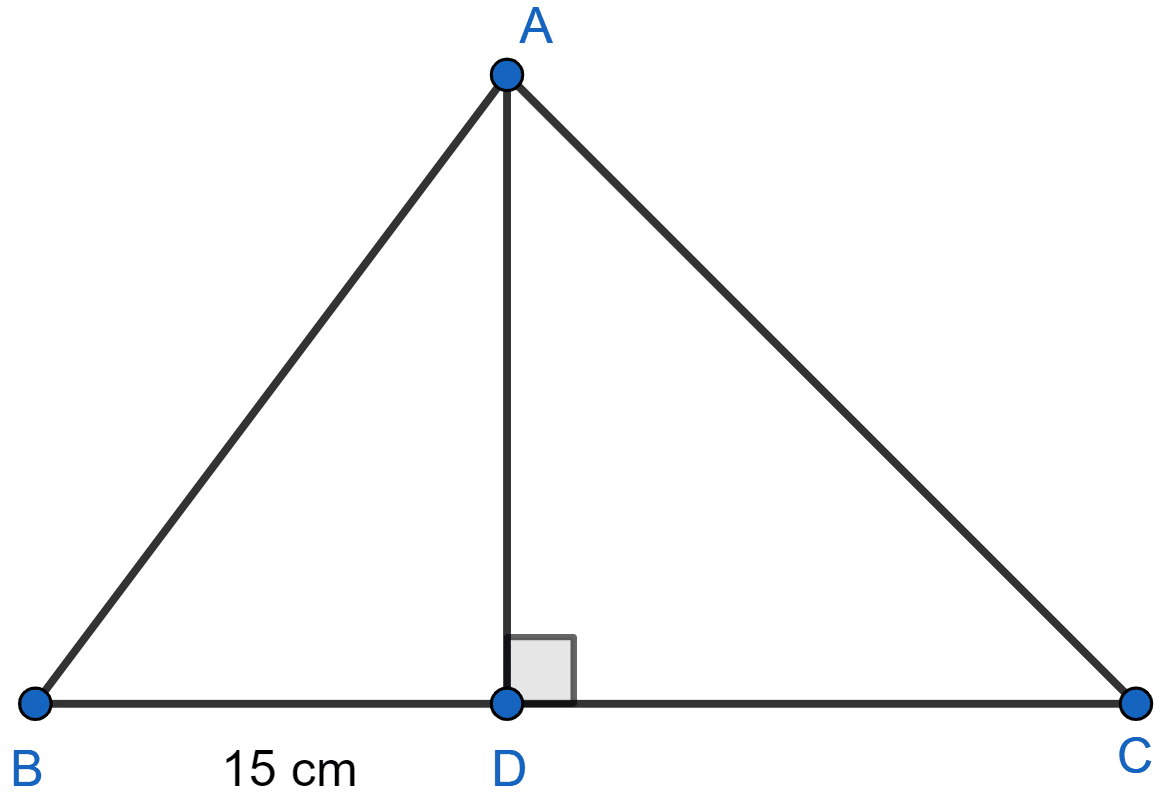
In the figure (3) given below, AD is perpendicular to BC, BD = 15 cm, sin B = and tan C = 1.
(i) Calculate the lengths of AD, AB, DC and AC.
(ii) Show that = -1.