Mathematics
Answer
∠1 = ∠4 (Vertically opposite angles)
⇒ 2∠2 = 2∠3
⇒ ∠2 = ∠3.
TS = TR (Given)
⇒ ∠TRS = ∠TSR (As angle opposite to equal side are equal)
⇒ ∠TRS - ∠2 = ∠TSR - ∠3
⇒ ∠ARB = ∠BSA.
∠RTB = ∠STA (Common angle)
△RBT ≅ △SAT (By ASA axiom.)
We know that corresponding sides of congruent triangles are equal.
∴ RB = SA.
Hence, proved that RB = SA.
Related Questions
In the adjoining figure, ABC is a right angled triangle at B. ADEC and BCFG are squares. Prove that AF = BE.

In the adjoining figure, BD= AD = AC. If ∠ABD = 36°, find the value of x.

In the figure (1) given below, find the value of x.

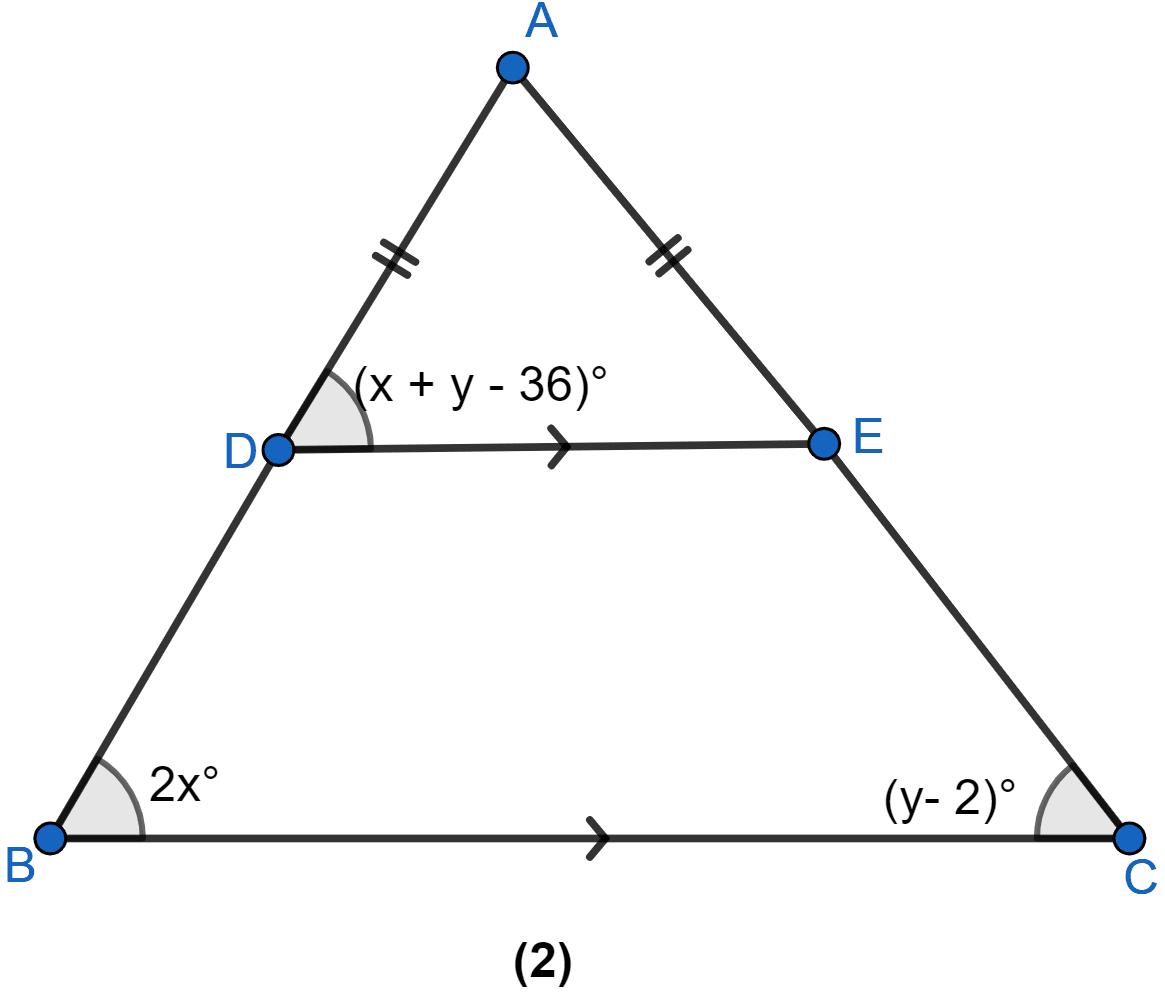
In the figure (2) given below, AB = AC and DE || BC. Calculate
(i) x
(ii) y
(iii) ∠BAC