Mathematics
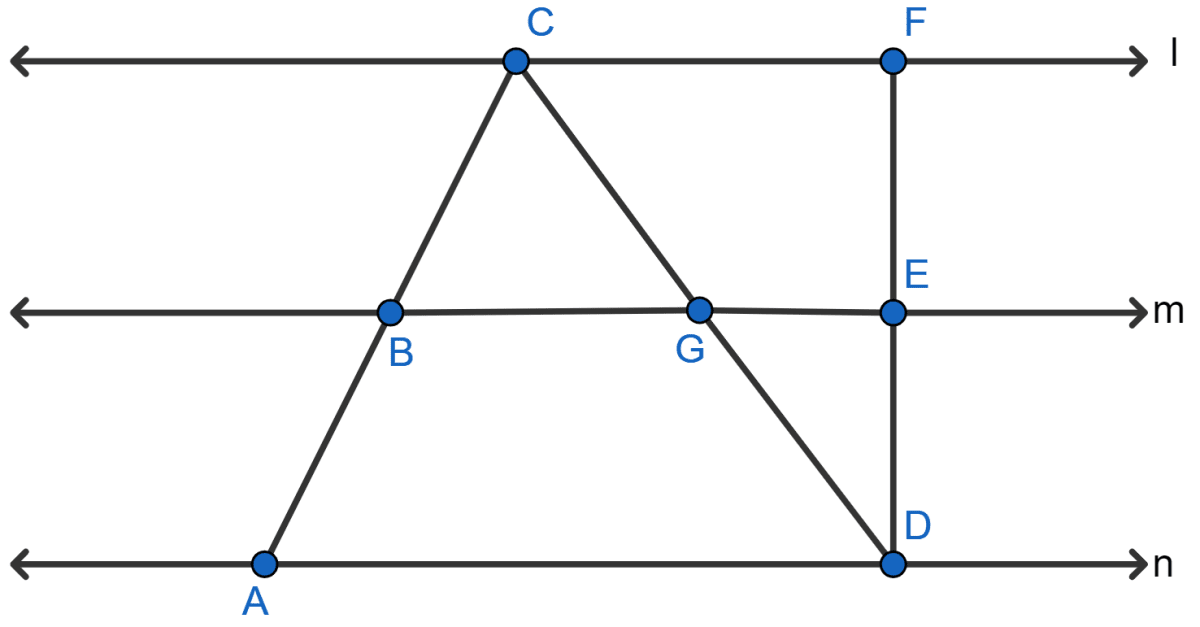
In the adjoining figure, the lines l, m and n are parallel to each other, and G is mid-point of CD. Calculate :
(i) BG if AD = 6 cm
(ii) CF if GE = 2.3 cm
(iii) AB if BC = 2.4 cm
(iv) ED if FD = 4.4 cm
Mid-point Theorem
44 Likes
Answer
(i) In △ACD,
G is mid-point of CD and BG is parallel to AD,
∴ B is mid-point of AC (By converse of mid-point theorem).
By mid-point theorem,
BG = AD = x 6 = 3 cm.
Hence, BG = 3 cm.
(ii) In △CDF,
G is mid-point of CD and GE || CF
∴ E is mid-point of FD (By converse of mid-point theorem).
By mid-point theorem,
GE = CF
CF = 2GE
CF = 2(2.3) = 4.6 cm
Hence, CF = 4.6 cm.
(iii) From part (i)
B is mid-point of AC,
∴ AB = BC
Hence, AB = 2.4 cm
(iv) From part (ii),
E is mid-point of FD,
∴ ED = FD = x 4.4 = 2.2 cm
Hence, ED = 2.2 cm
Answered By
30 Likes
Related Questions
In the quadrilateral given below, AD = BC, P, Q, R and S are mid-points of AB, BD, CD and AC respectively. Prove that PQRS is a rhombus.

In the figure given below, ABCD is a kite in which BC = CD, AB = AD. E, F, G are mid-points of CD, BC and AB respectively. Prove that :
(i) ∠EFG = 90°
(ii) The line drawn through G and parallel to FE bisects DA.

In a △ABC, AB = 3 cm, BC = 4 cm and CA = 5 cm. If D and E are mid-points of AB and BC respectively, then the length of DE is
1.5 cm
2 cm
2.5 cm
3.5 cm
In the adjoining figure, ABCD is a rectangle in which AB = 6 cm and AD = 8 cm. If P and Q are mid-points of the sides BC and CD respectively, then the length of PQ is
7 cm
5 cm
4 cm
3 cm
