Mathematics
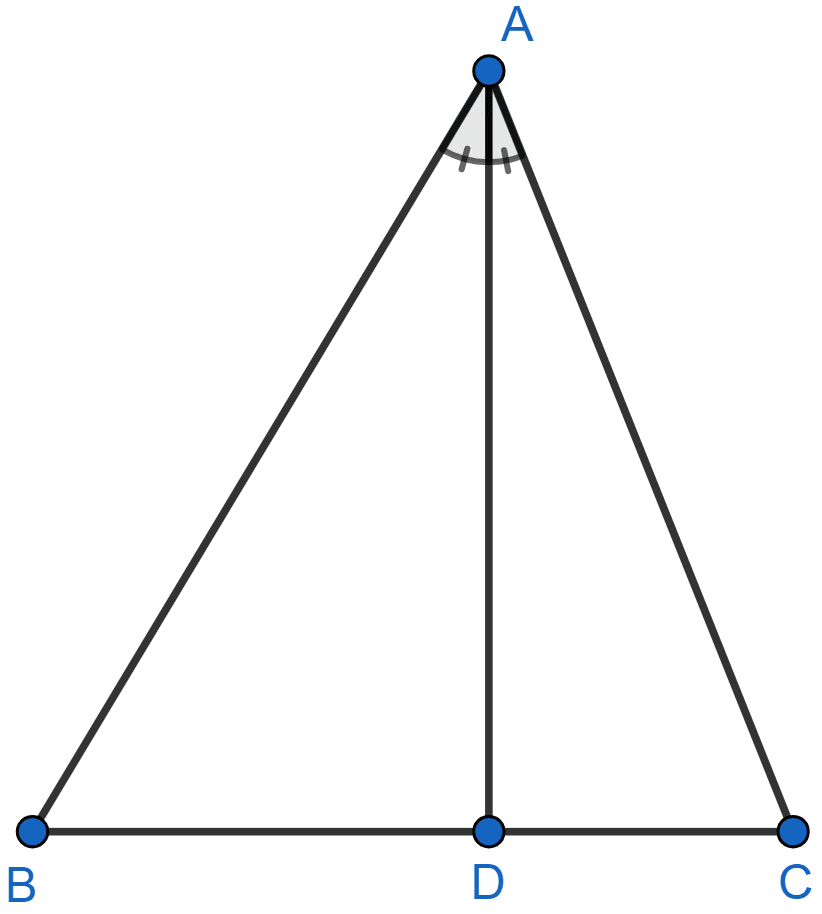
In the adjoining figure, AD is bisector of ∠BAC. If AB = 6 cm, AC = 4 cm and BD = 3 cm, find BC.
Similarity
79 Likes
Answer
We know that,
The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of the sides containing the angle.
.
Putting values in above equation we get,
BC = BD + DC = 3 + 2 = 5 cm.
Hence, the length of BC = 5 cm.
Answered By
47 Likes
Related Questions
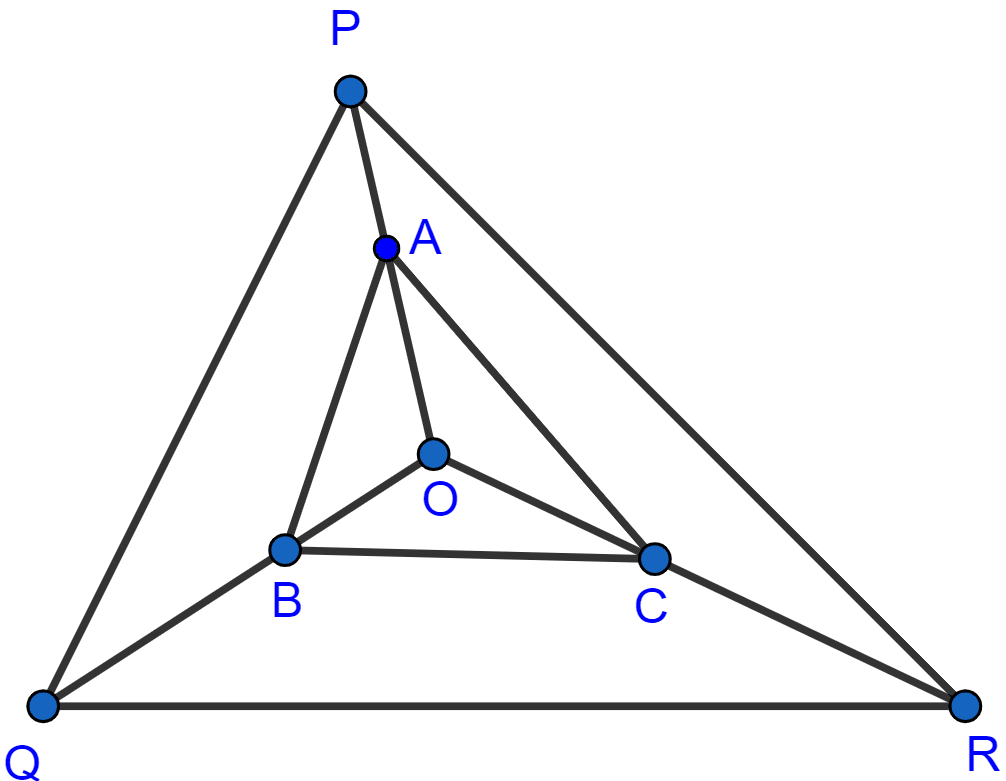
In the adjoining figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
ABCD is a trapezium in which AB || DC and its diagonals intersect each other at O. Using Basic Proportionality theorem prove that
Given that △s ABC and PQR are similar. Find :
(i) the ratio of the area of △ABC to the area of △PQR if their corresponding sides are in the ratio 1 : 3.
(ii) the ratio of their corresponding sides if area of △ABC : area of △PQR = 25 : 36.
△ABC ~ △DEF. If area of △ABC = 9 sq. cm, area of △DEF = 16 sq. cm and BC = 2.1 cm, find the length of EF.