Mathematics
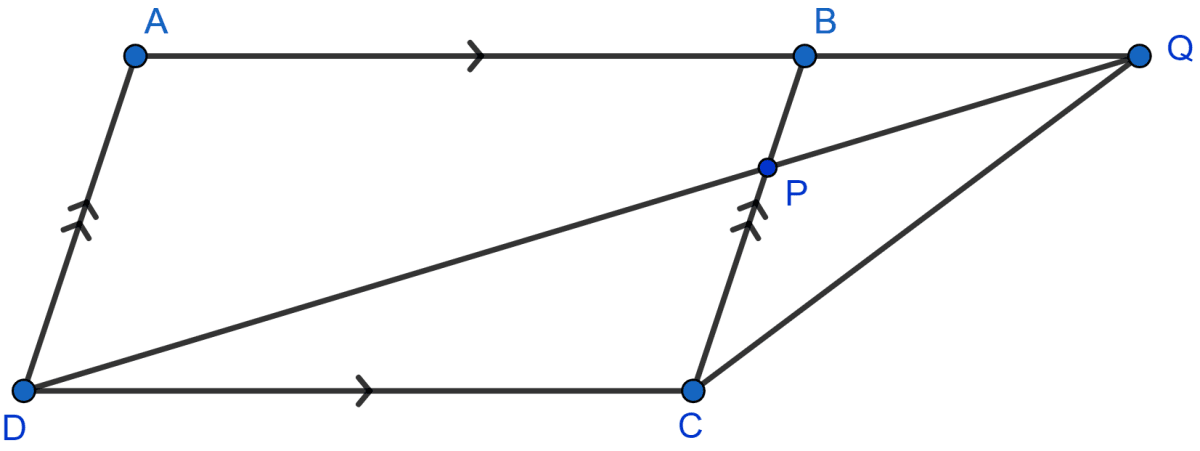
In the adjoining figure, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2 and DP produced meets AB produced at Q.
If area of △CPQ = 20 cm2, find
(i) area of △BPQ.
(ii) area of △CDP.
(iii) area of ||gm ABCD.
Similarity
54 Likes
Answer
(i) Draw QN ⊥ CB as shown in the figure below:
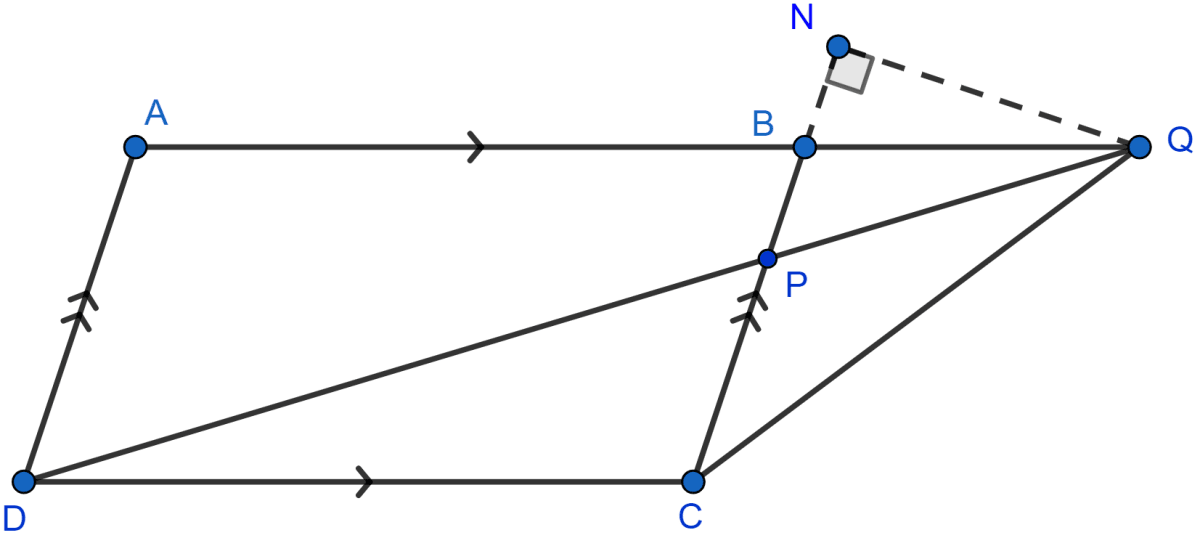
Hence, the area of △BPQ = 10 cm2.
(ii) Considering △CDP and △BQP,
∠CPD = ∠QPB (Vertically opposite angles are equal)
∠PDC = ∠PQB (Alternate angles are equal)
Hence, by AA axiom △CDP ~ △BQP.
We know that, the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.
∴ Area of △CDP = 4 × Area of △BQP = 4 × 10 = 40 cm2.
Hence, the area of △CDP = 40 cm2.
(iii) Area of ||gm ABCD = 2 Area of △DCQ (As △DCQ and ||gm ABCD have same base and are between same parallels)
Hence, the area of ||gm = 120 cm2.
Answered By
32 Likes
Related Questions
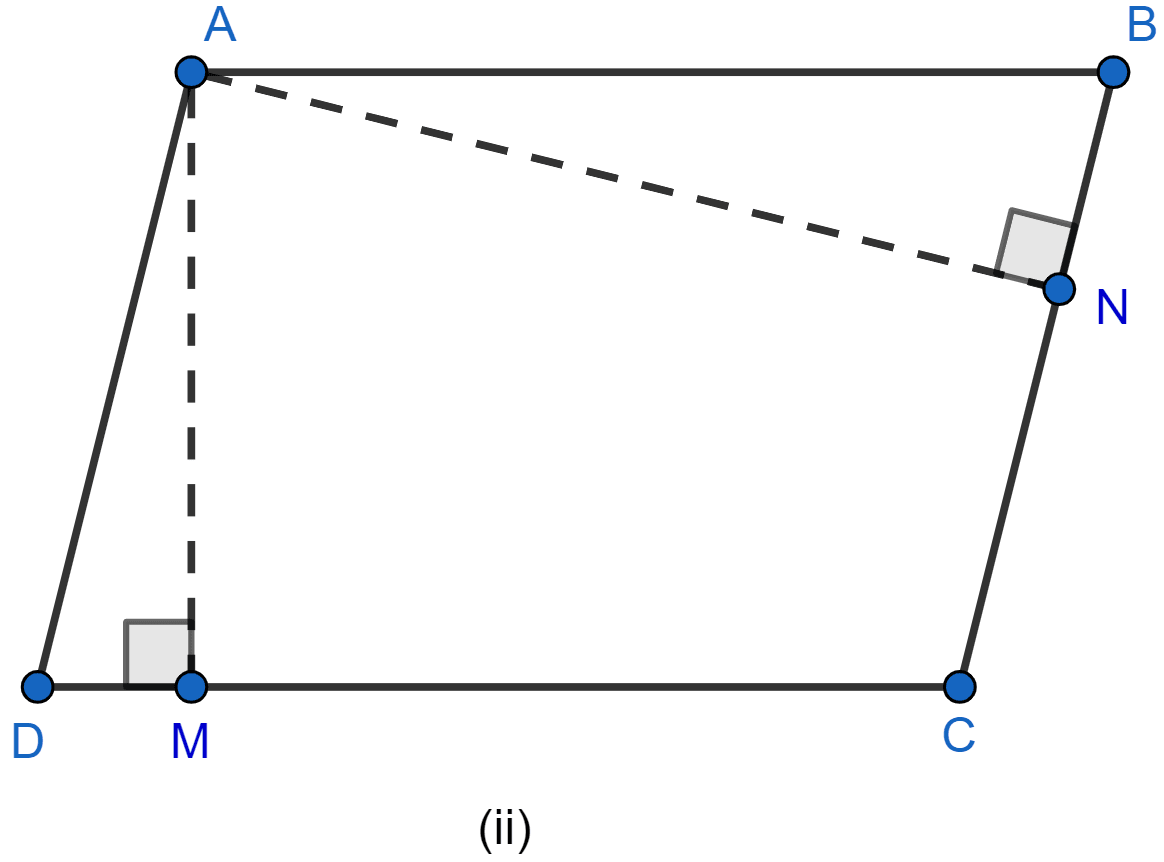
In the figure (ii) given below, ABCD is a parallelogram. AM ⊥ DC and AN ⊥ CB. If AM = 6 cm, AN = 10 cm and the area of parallelogram ABCD is 45 cm2, find
(i) AB
(ii) BC
(iii) area of △ADM : area of △ANB.
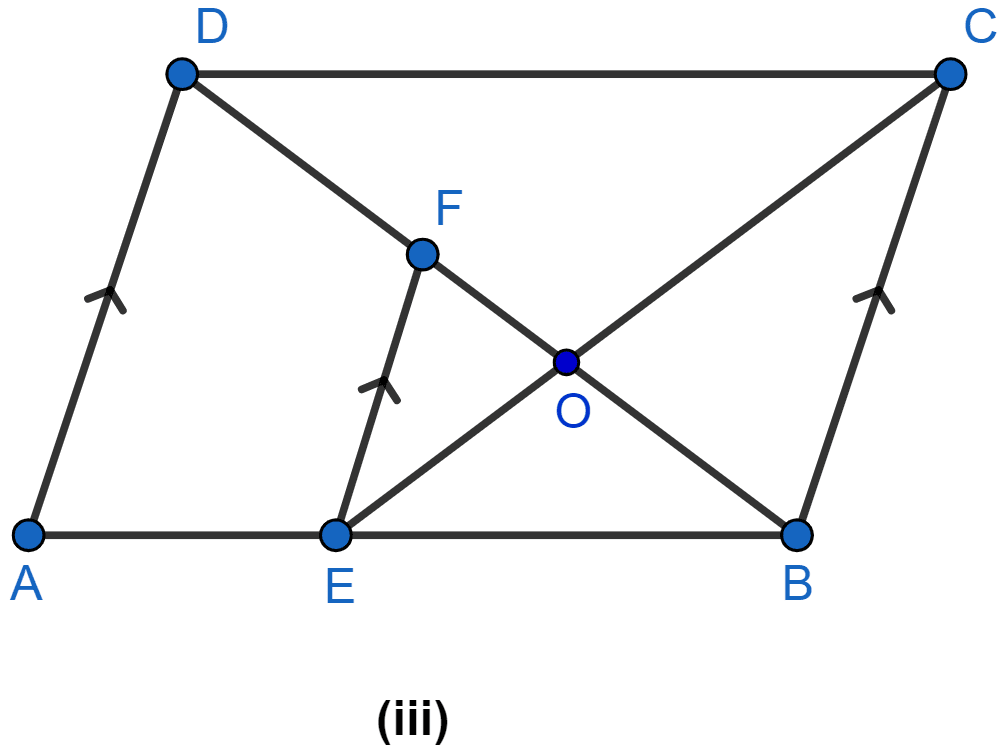
In the figure (iii) given below, ABCD is a parallelogram. E is a point on AB, CE intersects the diagonal BD at O and EF || BC. If AE : EB = 2 : 3, find
(i) EF : AD
(ii) area of △BEF : area of △ABD
(iii) area of △ABD : area of trap. AEFD
(iv) area of △FEO : area of △OBC.
In the figure (i) given below, DE || BC and the ratio of the areas of △ADE and trapezium DBCE is 4 : 5. Find the ratio of DE : BC.

In the figure (ii) given below, AB || DC and AB = 2DC. If AD = 3 cm, BC = 4 cm and AD, BC produced meet at E, find
(i) ED
(ii) BE
(iii) area of △EDC : area of trapezium ABCD.
