Mathematics
In the adjoining figure, AB = CD, CE = BF and ∠ACE = ∠DBF. Prove that
(i) △ACE ≅ △DBF
(ii) AE = DF.

Triangles
76 Likes
Answer
(i) In △ACE and △DBF,
Given,
AB = CD
⇒ AB + BC = CD + BC
⇒ AC = BD.
∠ACE = ∠DBF (Given)
CE = BF (Given)
Hence, by SAS axiom △ACE ≅ △DBF.
(ii) We know that, △ACE ≅ △DBF.
We know that corresponding sides of congruent triangles are equal.
∴ AE = DF.
Hence, proved that AE = DF.
Answered By
40 Likes
Related Questions
In the adjoining figure, AB = AC and D is the midpoint of BC. Use SSS rule of congruency to show that
(i) △ABD ≅ △ACD
(ii) AD is bisector of ∠A
(iii) AD is perpendicular to BC.

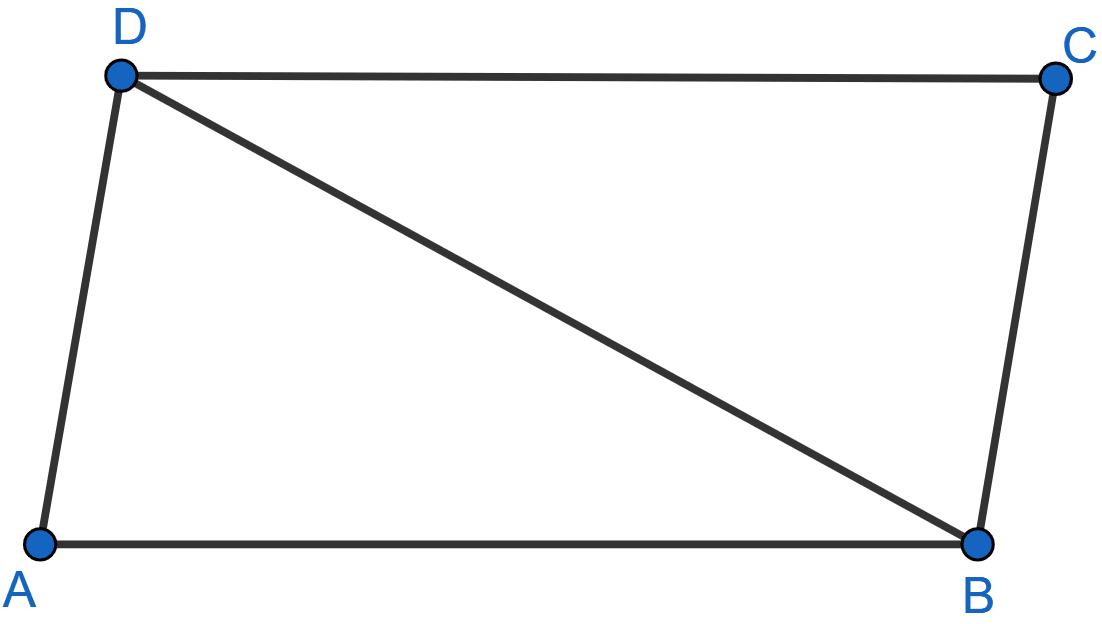
In the adjoining figure, AB = DC and AB || DC. Prove that AD = BC.
In the adjoining figure AC = AE, AB = AD and ∠BAD = ∠CAE. Show that BC = DE.

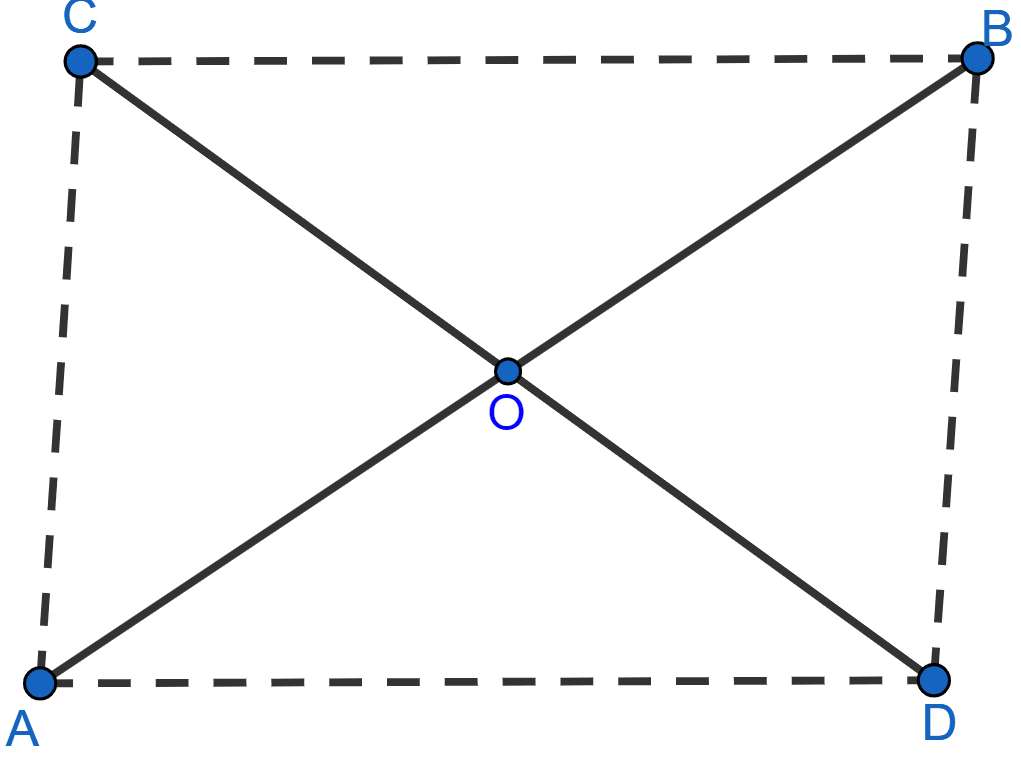
Two line segments AB and CD bisect each other at O. Prove that
(i) AC = BD
(ii) ∠CAB = ∠ABD
(iii) AD || CB
(iv) AD = CB