Mathematics
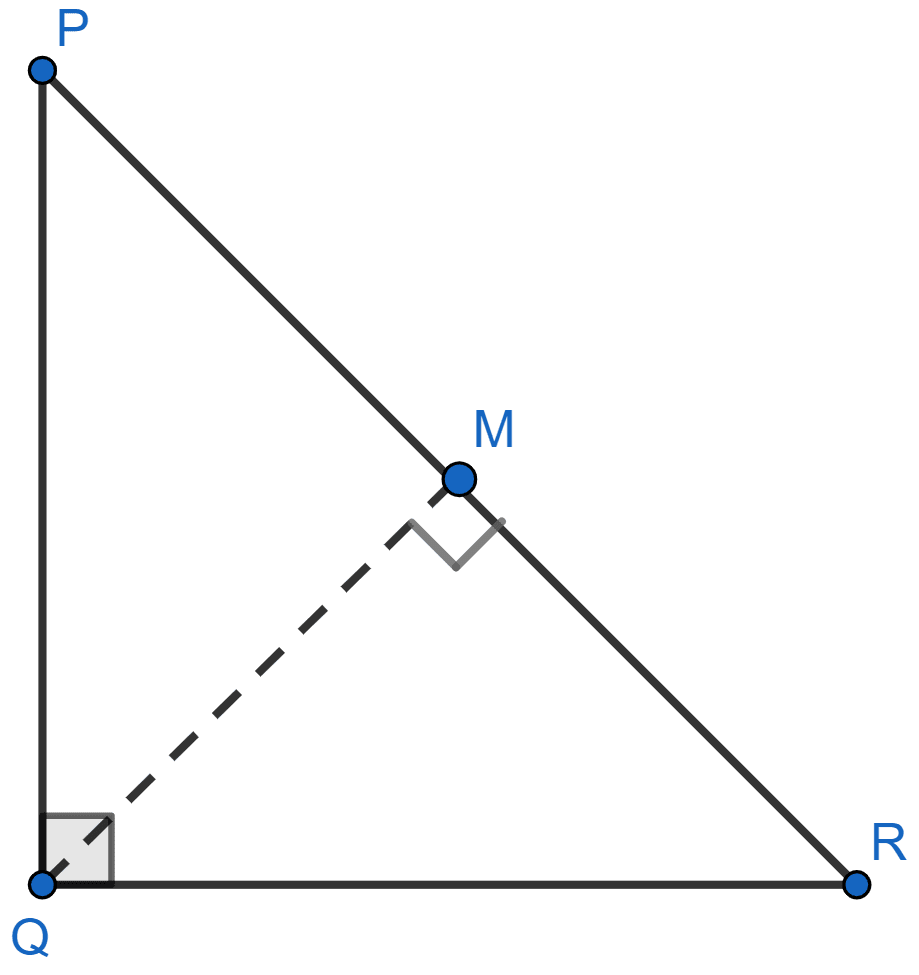
In △PQR, ∠Q = 90° and QM is perpendicular to PR. Prove that :
(i) PQ2 = PM × PR
(ii) QR2 = PR × MR
(iii) PQ2 + QR2 = PR2
Similarity
43 Likes
Answer
△PQR is shown in the figure below:
(i) In △PQR and △PMQ,
⇒ ∠PMQ = ∠PQR [Both = 90°]
⇒ ∠QPM = ∠RPQ [Common]
∴ △PQR ~ △PMQ [By AA]
Since, corresponding sides of similar triangles are proportional we have :
⇒
⇒ PQ2 = PM × PR
Hence, proved that PQ2 = PM × PR.
(ii) In △QRM and △PRQ,
⇒ ∠QMR = ∠PQR [Both = 90°]
⇒ ∠QRM = ∠QRP [Common]
∴ △QRM ~ △PRQ [By AA]
Since, corresponding sides of similar triangles are proportional we have :
⇒
⇒ QR2 = PR × MR
Hence, proved that QR2 = PR × MR.
(iii) Adding equations from (i) and (ii) we get,
⇒ PQ2 + QR2 = PM × PR + PR × MR ………(1)
⇒ PQ2 + QR2 = PR(PM + MR)
From figure,
PM + MR = PR
⇒ PQ2 + QR2 = PR2.
Hence, proved that PQ2 + QR2 = PR2.
Answered By
28 Likes
Related Questions
In ΔABC, BM ⊥ AC and CN ⊥ AB; show that:
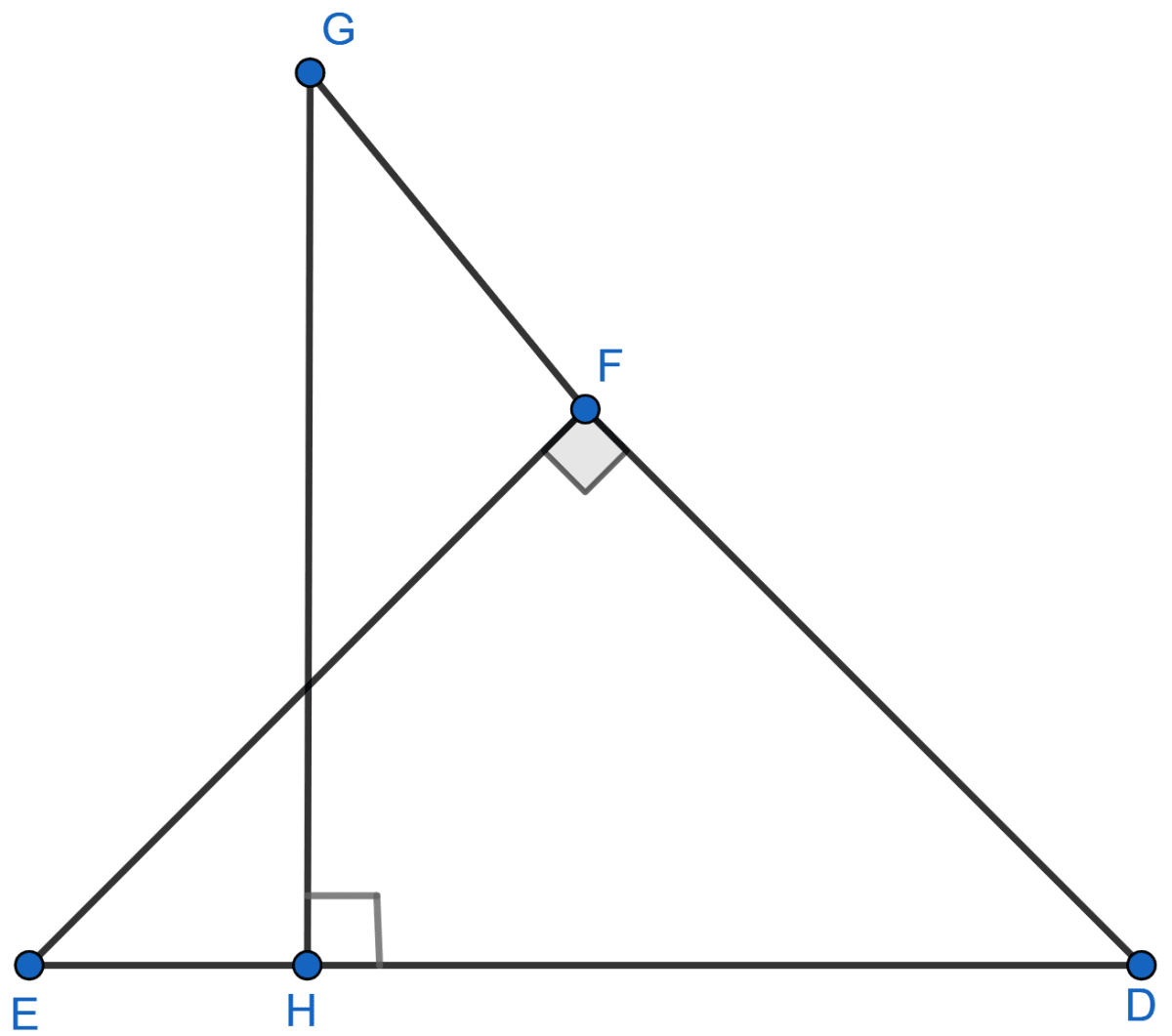
Given: ∠GHE = ∠DFE = 90°, DH = 8, DF = 12, DG = 3x – 1 and DE = 4x + 2.
Find: the lengths of segments DG and DE.
In △ABC, ∠B = 90° and BD ⊥ AC.
(i) If CD = 10 cm and BD = 8 cm; find AD.
(ii) If AC = 18 cm and AD = 6 cm; find BD.
(iii) If AC = 9 cm and AB = 7 cm; find AD.
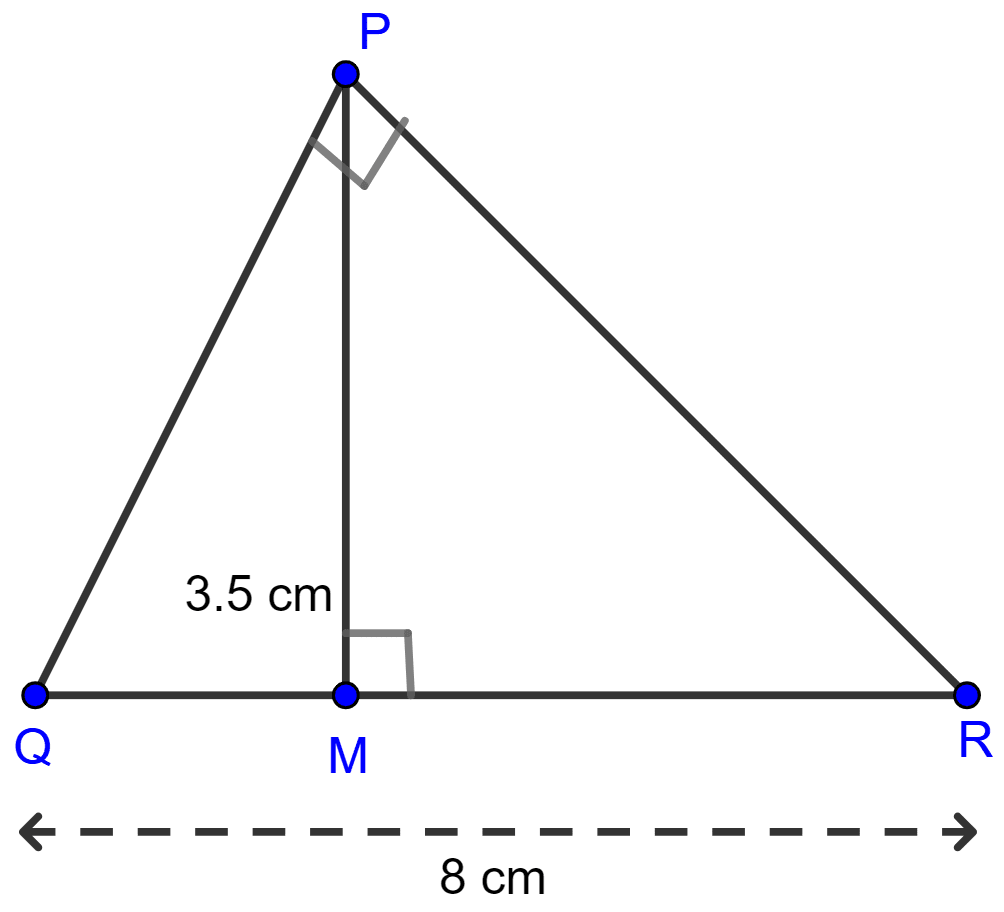
In the right-angled triangle QPR. PM is an altitude.
Given that QR = 8 cm and MQ = 3.5 cm, calculate the value of PR.