Mathematics
In parallelogram ABCD, A = (6, 0), B = (12, -4) and C = (4, -4); then the co-ordinates of vertex D are :
(2, 0)
(-2, 0)
(0, 2)
(0, -2)
Section Formula
12 Likes
Answer
Let co-ordinates of vertex D be (x, y).
We know that,
Diagonal of parallelogram bisect each other.
From figure,
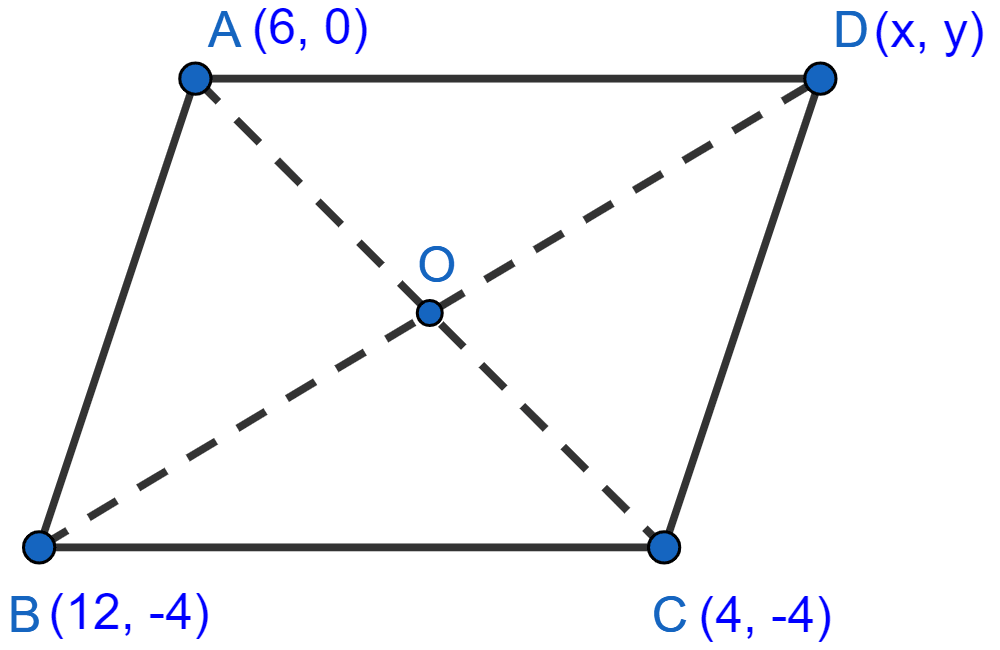
O (a, b) is the mid-point of AC.
By mid-point formula,
Mid-point =
Substituting values we get :
From figure,
O is also the mid-point of BD.
D = (-2, 0).
Hence, Option 2 is the correct option.
Answered By
3 Likes
Related Questions
The point P(2, -7) is reflected in the point (0, 3); the co-ordinates of the image of point P are :
(2, 13)
(2, -13)
(-2, -13)
(-2, 13)
The co-ordinates of the centroid of a triangle with vertices (-6, -3), (0, 0) and (12, -6) are :
(2, 3)
(-2, 3)
(2, -3)
(-2, -3)
Point A(3, 4) is the center of a circle. If one of its diameters has one end as (7, 8); the other end of this diameter is :
(1, 0)
(0, 1)
(-1, 0)
(0, -1)
Point A lies on x-axis and point B lies on y-axis. If P(2, -2) bisects the line segment AB, the co-ordinates of A are :
(4, 0)
(0, 4)
(-4, 0)
(0, -4)