Mathematics

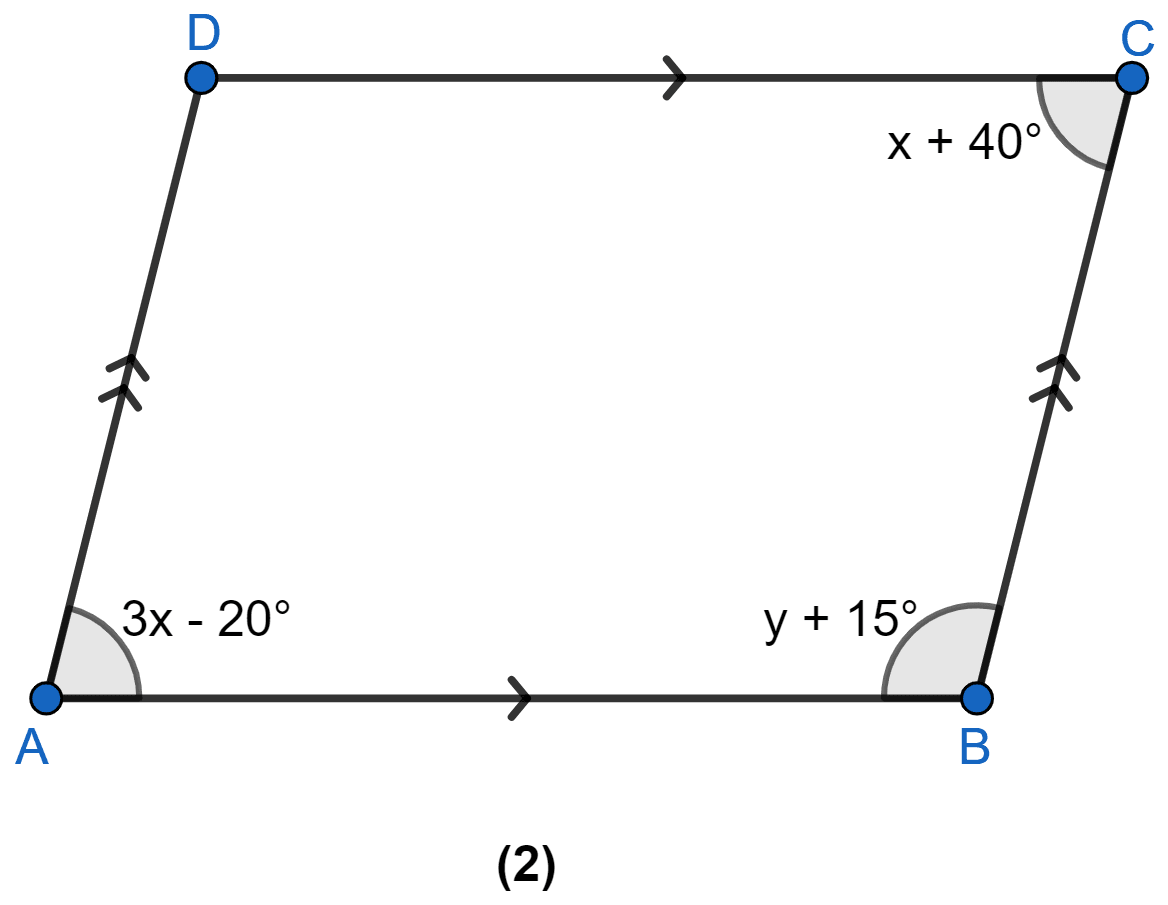
In figure (2) given below, ABCD is a parallelogram. Find the values of x and y.

Rectilinear Figures

34 Likes

Answer

In parallelogram,

Opposite angles are equal

∴ ∠A = ∠C

⇒ 3x - 20° = x + 40°

⇒ 3x - x = 40° + 20°

⇒ 2x = 60°

⇒ x = 30°.

As AD || BC, sum of co-int ∠s = 180°.

⇒ ∠A + ∠B = 180°

⇒ 3x - 20° + y + 15° = 180°

⇒ 3(30°) - 20° + y + 15° = 180°

⇒ 90° - 20° + y + 15° = 180°

⇒ 85° + y = 180°

⇒ y = 95°.

Hence, x = 30° and y = 95°.

Answered By

23 Likes

Related Questions

In figure (1) given below, ABCD is a parallelogram with perimeter 40. Find the values of x and y.
View Answer