Mathematics
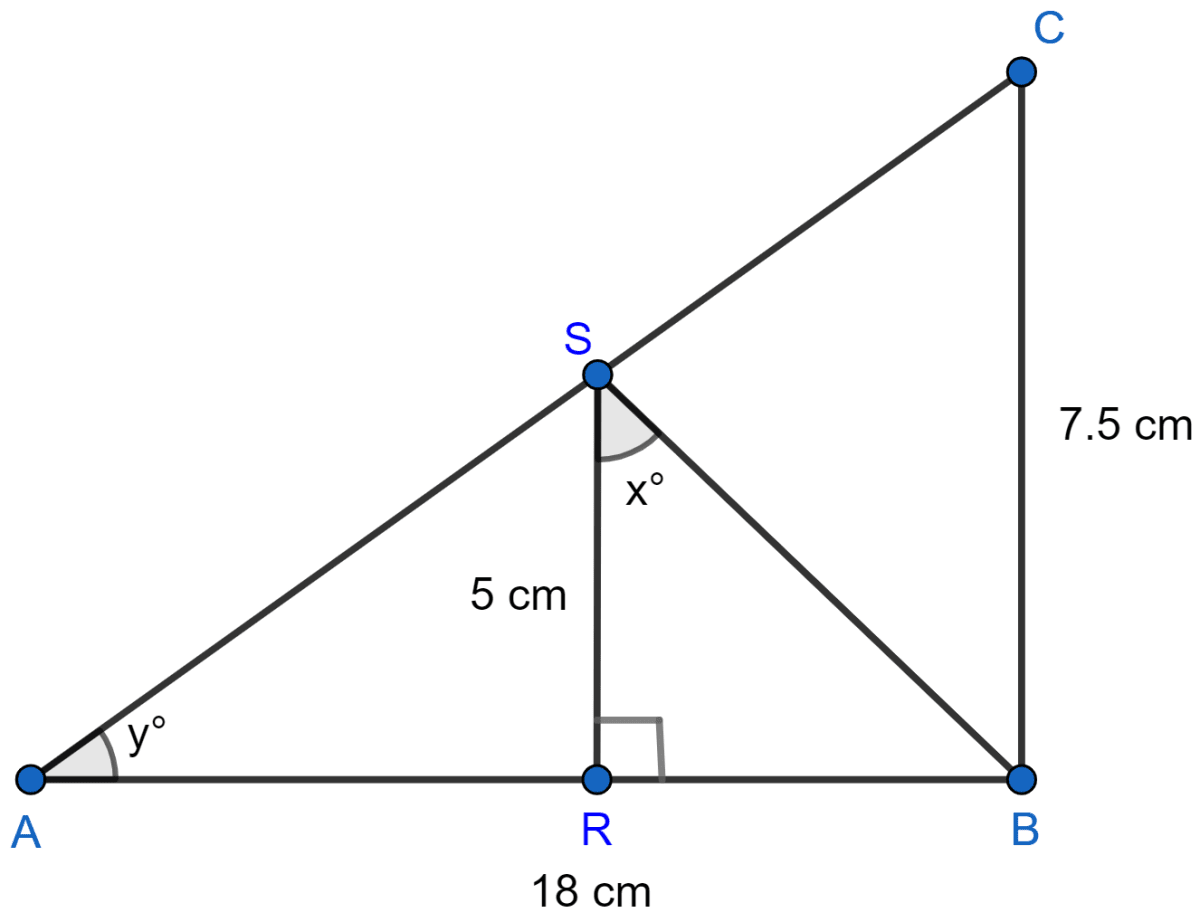
In figure (1) given below, ∆ABC is right-angled at B and ∆BRS is right-angled at R. If AB = 18 cm, BC = 7.5 cm, RS = 5 cm, ∠BSR = x° and ∠SAB = y°, then find :
(i) tan x°
(ii) sin y°.
Trigonometrical Ratios
46 Likes
Answer
In ∆ARS and ∆ABC,
∠ARS = ∠ABC (Both = 90°)
∠SAR = ∠CAB (Common)
∴ ∆ARS ~ ∆ABC [By AA axiom]
∴
Substituting the values we get,
From figure,
RB = AB - AR = 18 - 12 = 6.
In right-angled ∆ABC,
⇒ AC2 = AB2 + BC2 [By pythagoras theorem]
⇒ AC2 = 182 + (7.5)2
⇒ AC2 = 324 + 56.25 = 380.25
⇒ AC = = 19.5 cm.
(i) In right-angled ∆BSR,
tan x° =
= .
Hence, tan x° = .
(ii) In right-angled ∆ABC,
sin y° =
= =
= =
Hence, sin y° = .
Answered By
24 Likes
Related Questions
Prove the following :
If in ∆ABC, ∠C = 90° and tan A = , prove that
sin A cos B + cos A sin B = 1.
In the figure (2) given below, ∆ABC is right-angled at B and BD is perpendicular to AC. Find :
(i) cos ∠CBD
(ii) cot ∠ABD

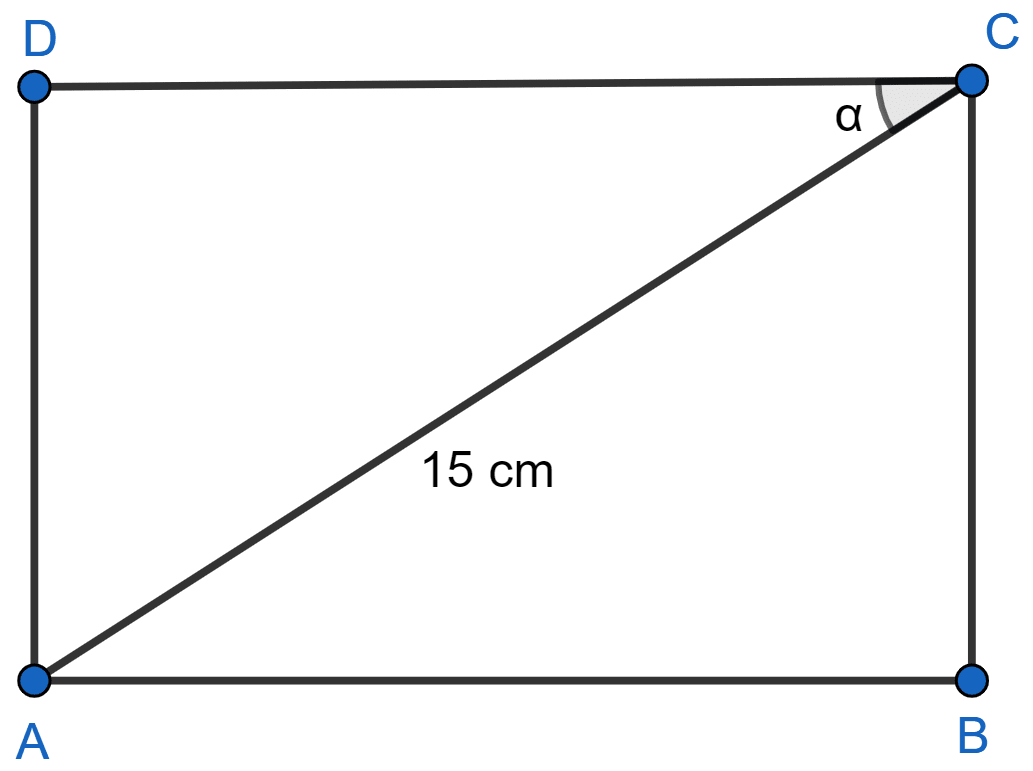
In the adjoining figure, ABCD is a rectangle. Its diagonal AC = 15 cm and ∠ACD = α. If cot α = , find the perimeter and the area of the rectangle.