Mathematics
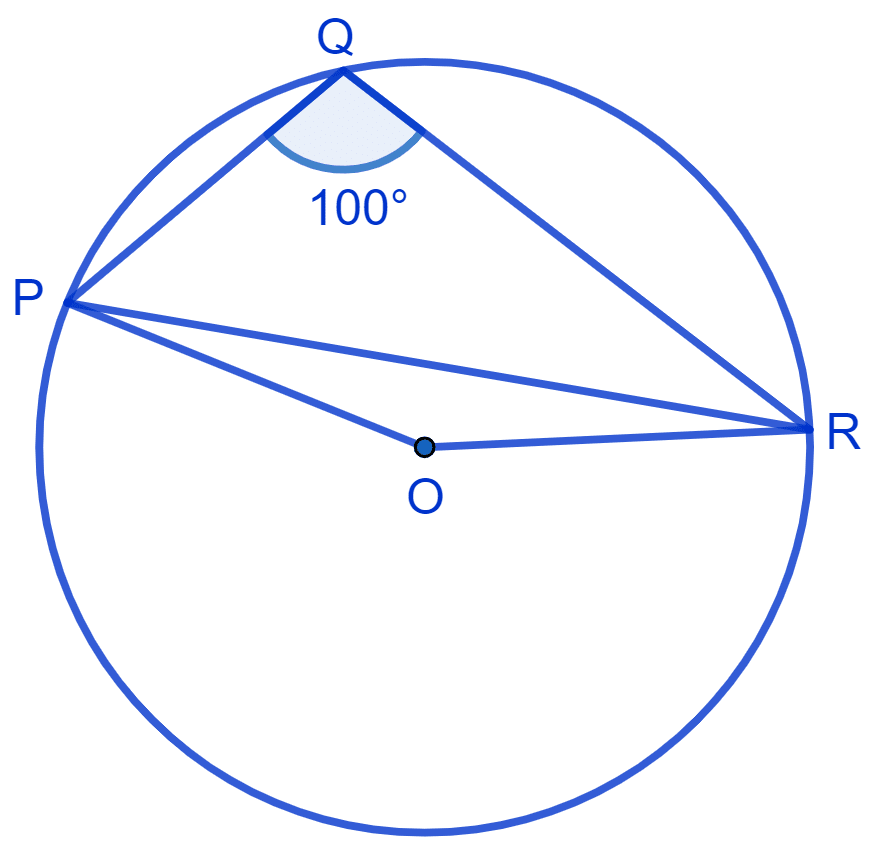
In Fig. ∠PQR = 100°, where P, Q and R are points on a circle with centre O. Find ∠OPR.
Circles
3 Likes
Answer
From figure,
Consider PR as a chord of the circle.
Steps of construction :
Mark any point S on the major arc of the circle. (on the side opposite to point Q)
Join PS and SR.
PQRS is a cyclic quadrilateral.
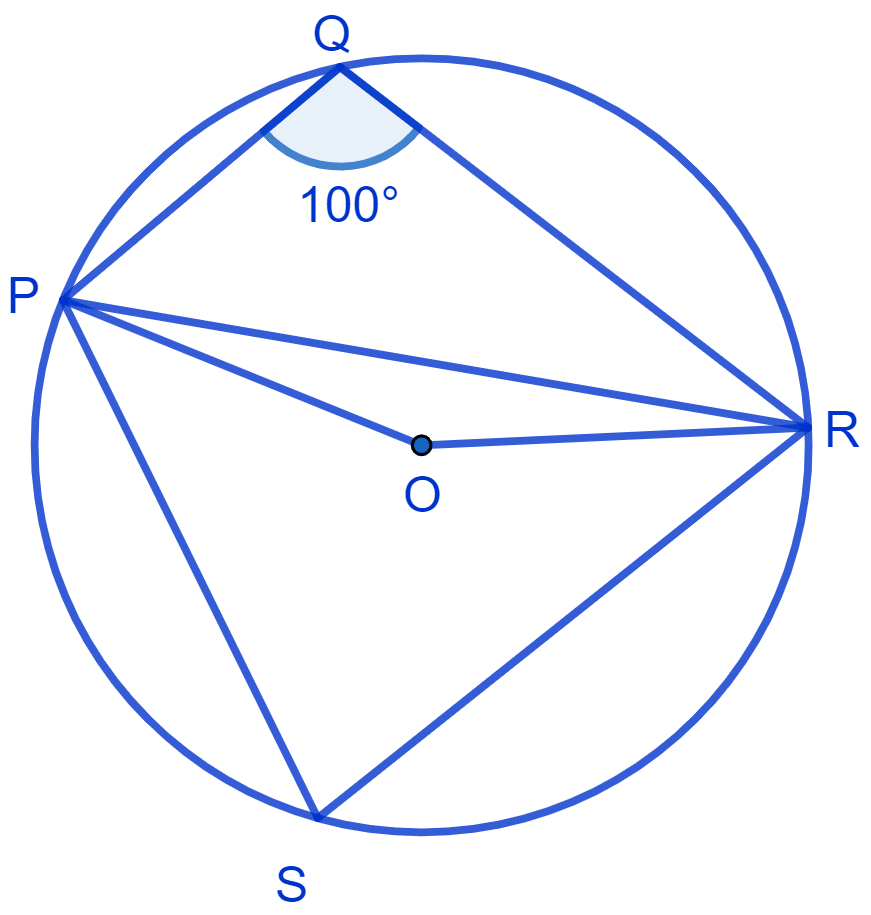
⇒ ∠PQR + ∠PSR = 180° (Sum of opposite angles in a cyclic quadrilateral = 180°)
⇒ 100° + ∠PSR = 180°
⇒ ∠PSR = 180° - 100° = 80°.
We know that,
The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
∴ ∠POR = 2∠PSR
⇒ ∠POR = 2 × 80°
⇒ ∠POR = 160°.
In ∆ OPR,
⇒ OP = OR (Radius of the circle)
We know that,
Angles opposite to equal sides are equal.
∴ ∠OPR = ∠ORP = a (let).
We know that,
Sum of all angles in a triangle is 180°.
⇒ ∠OPR + ∠POR + ∠ORP = 180°
⇒ a + 160° + a = 180° [∵ ∠OPR = ∠ORP]
⇒ 2a = 180° - 160°
⇒ 2a = 20°
⇒ a = = 10°
⇒ ∠OPR = 10°.
Hence, ∠OPR = 10°.
Answered By
2 Likes
Related Questions
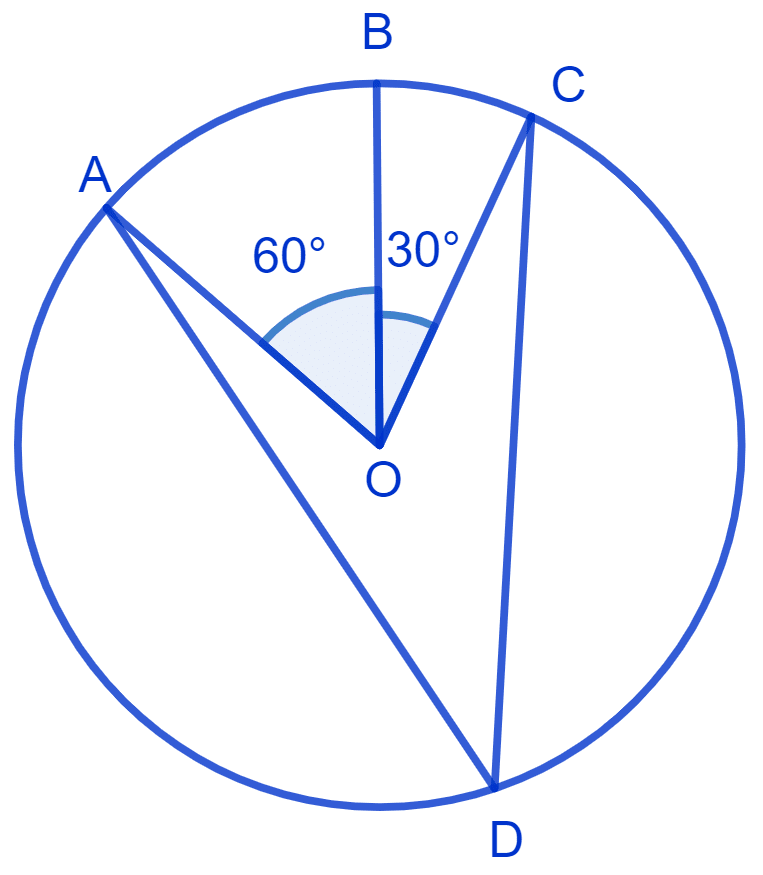
In Fig. A, B and C are three points on a circle with centre O such that ∠BOC = 30° and ∠AOB = 60°. If D is a point on the circle other than the arc ABC, find ∠ADC.
A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
In Fig. ∠ABC = 69°, ∠ACB = 31°, find ∠BDC.
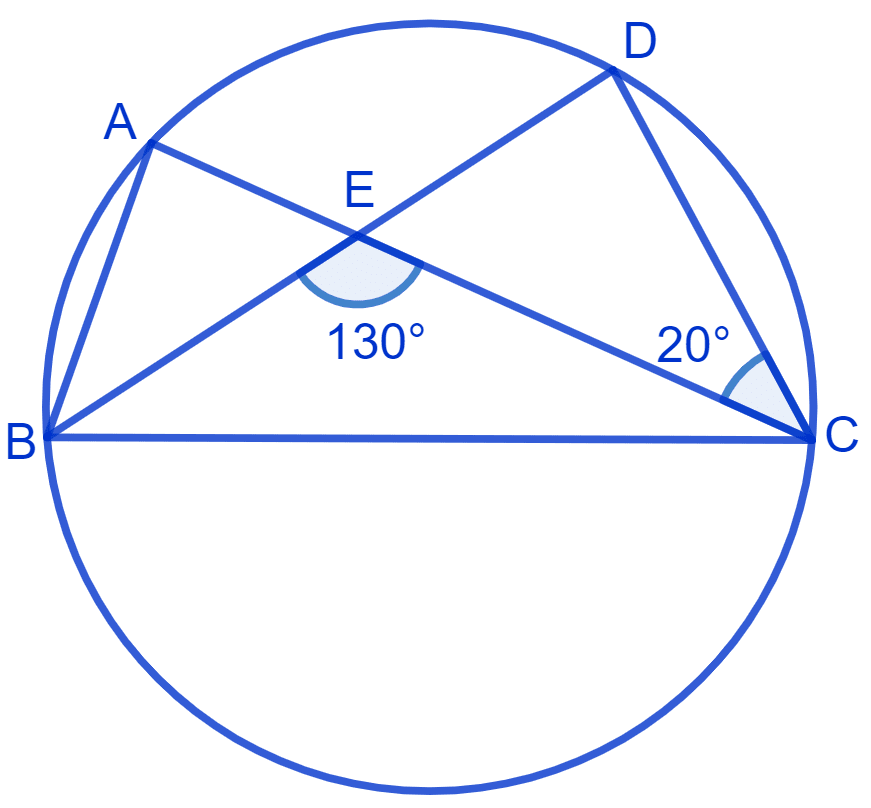
In Fig. A, B, C and D are four points on a circle. AC and BD intersect at a point E such that ∠BEC = 130° and ∠ECD = 20°. Find ∠BAC.