Mathematics
In each of the given figures; PA = PB and QA = QB.
(i)
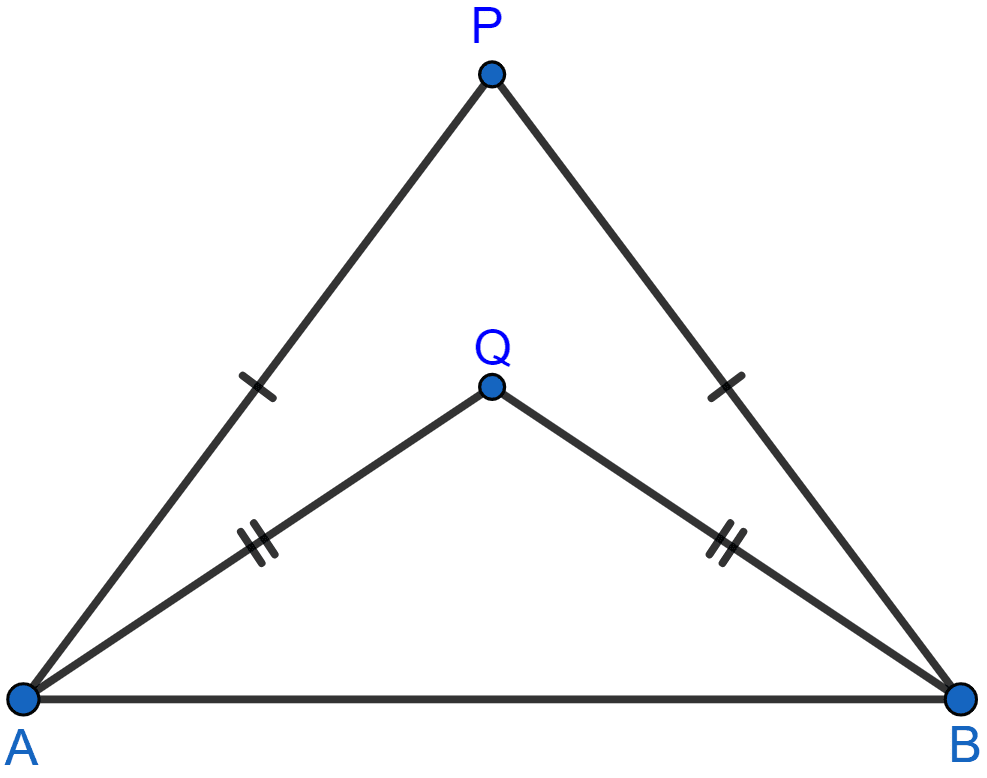
(ii)
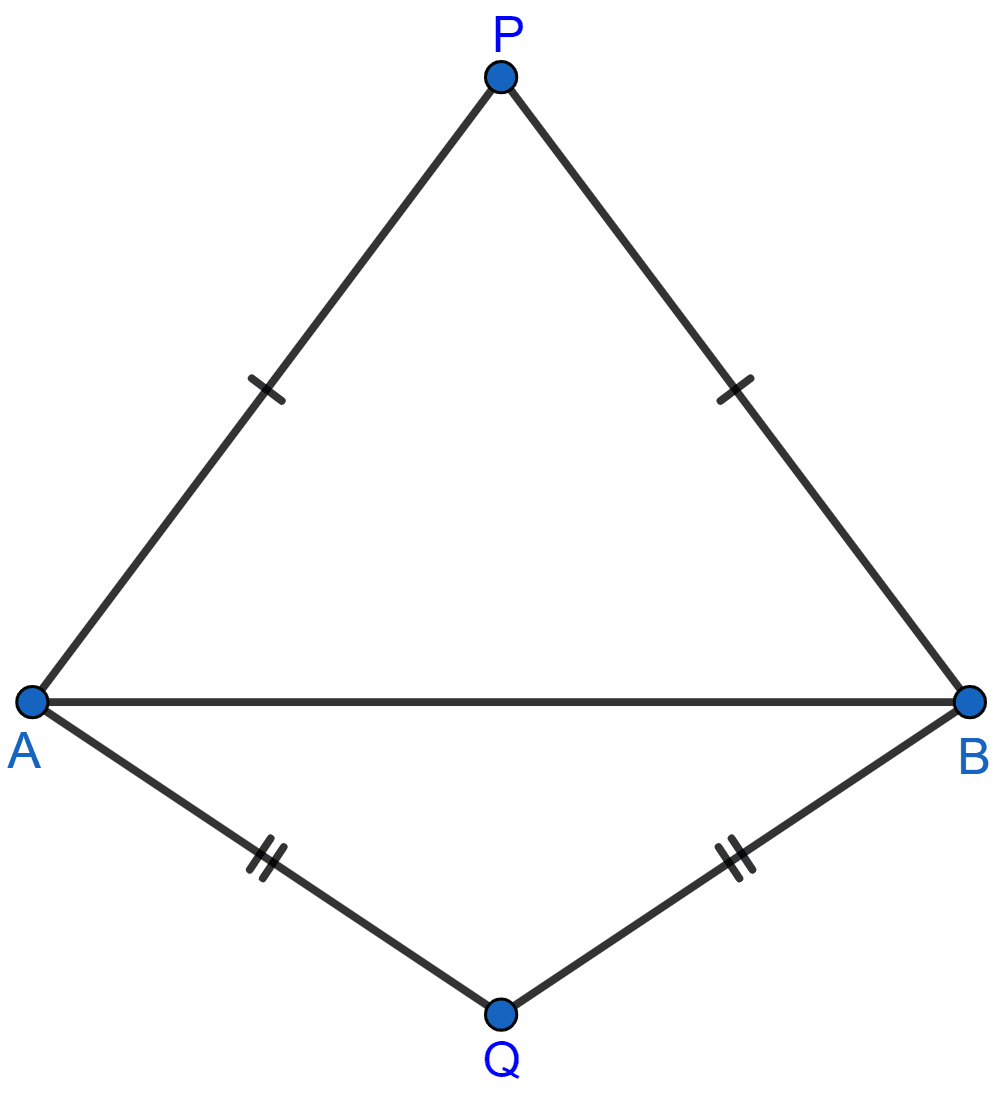
Prove in each case, that PQ (produce, if required) is perpendicular bisector of AB.
Hence, state the locus of the points equidistant from two given fixed points.
Locus
24 Likes
Answer
(i) Join PQ which meets AB in D.
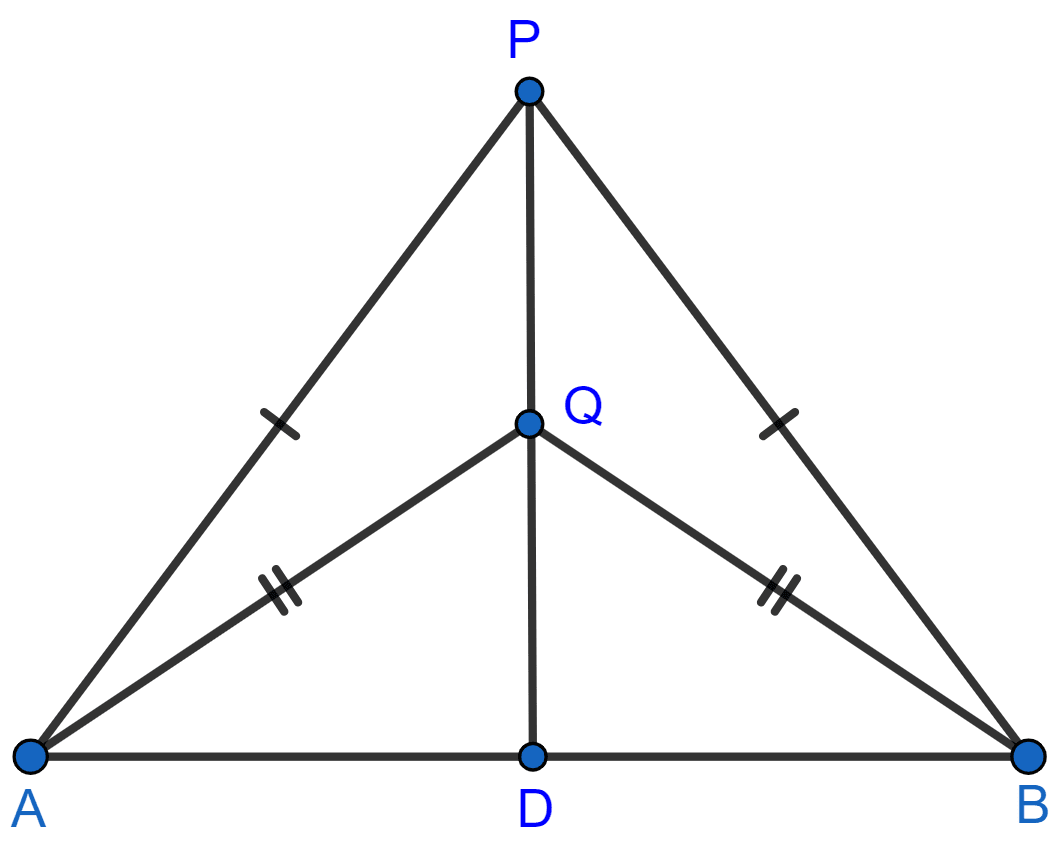
Given, PA = PB.
∴ P is equidistant from A and B. Thus, P lies on the perpendicular bisector of AB.
Given, QA = QB.
∴ Q is equidistant from A and B. Thus, Q lies on perpendicular bisector of AB.
Thus, both P and Q lie on the perpendicular bisector of AB.
Hence, proved that PQ is the perpendicular bisector of AB.
(ii) Join PQ which meets AB in D.
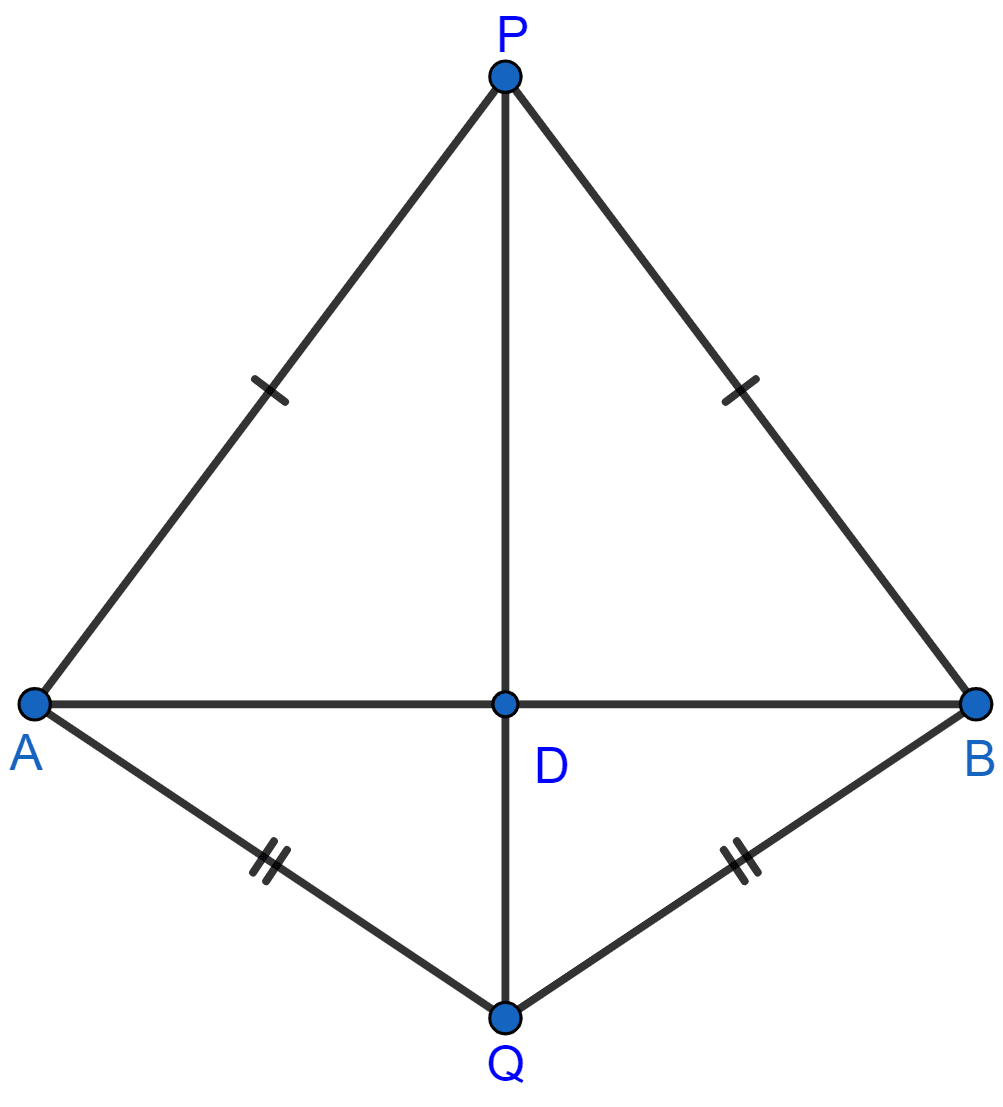
Given, PA = PB.
∴ P is equidistant from A and B. Thus, P lies on the perpendicular bisector of AB.
Given, QA = QB.
∴ Q is equidistant from A and B. Thus, Q lies on perpendicular bisector of AB.
Thus, both P and Q lie on the perpendicular bisector of AB.
Hence, proved that PQ is the perpendicular bisector of AB.
Hence, locus of the points which are equidistant from two fixed points, is the perpendicular bisector of the line joining the fixed points.
Answered By
18 Likes
Related Questions
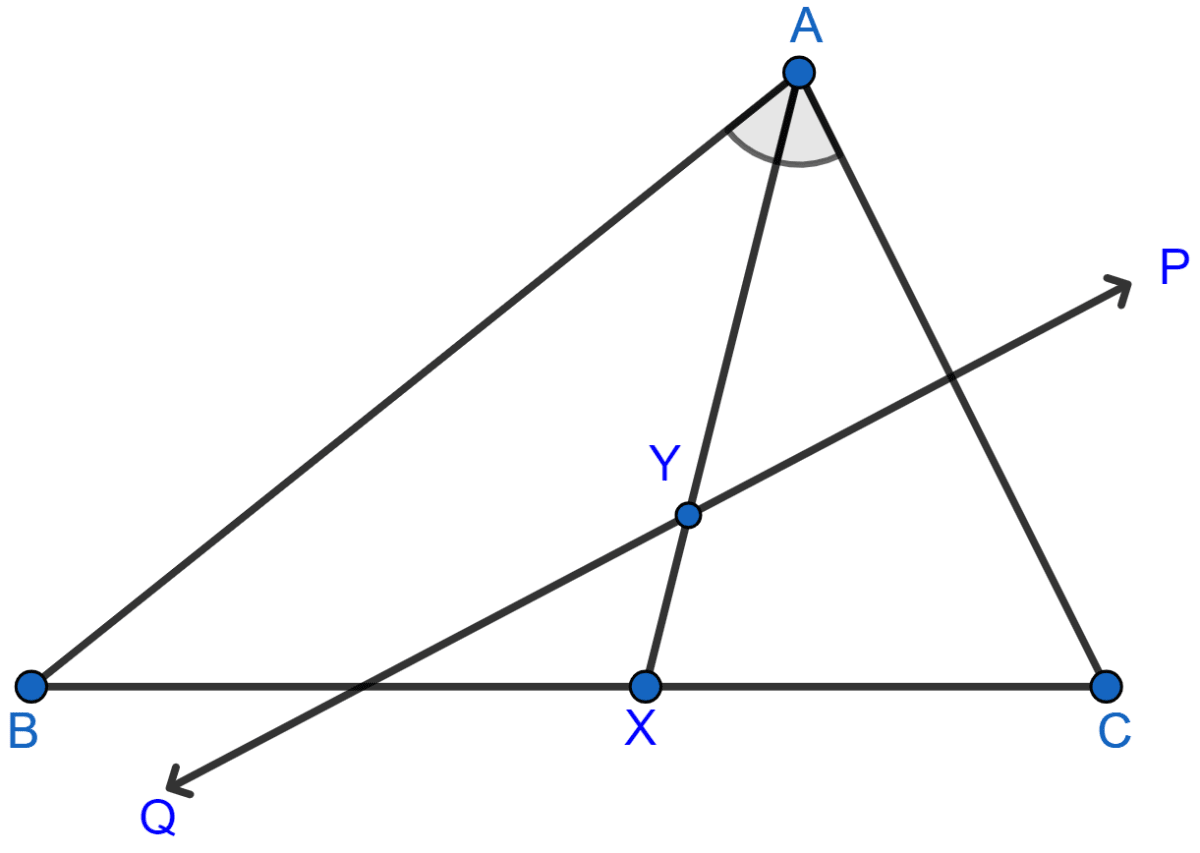
Given: AX bisects angle BAC and PQ is perpendicular bisector of AC which meets AX at point Y.
Prove :
(i) X is equidistant from AB and AC.
(ii) Y is equidistant from A and C.
In parallelogram ABCD, side AB is greater than side BC and P is a point in AC such that PB bisects angle B. Prove that P is equidistant from AB and BC.
Construct a triangle ABC, in which AB = 4.2 cm, BC = 6.3 cm and AC = 5 cm. Draw perpendicular bisector of BC which meets AC at point D. Prove that D is equidistant from B and C.
Construct a triangle ABC in which angle ABC = 75°, AB = 5 cm and BC = 6.4 cm. Draw perpendicular bisector of side BC and also the bisector of angle ACB. If these bisectors intersect each other at point P; prove that P is equidistant from B and C; and also from AC and BC.