Mathematics
In a cyclic quadrilateral ABCD, the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
Answer
We know that,
Angles in same segment are equal.
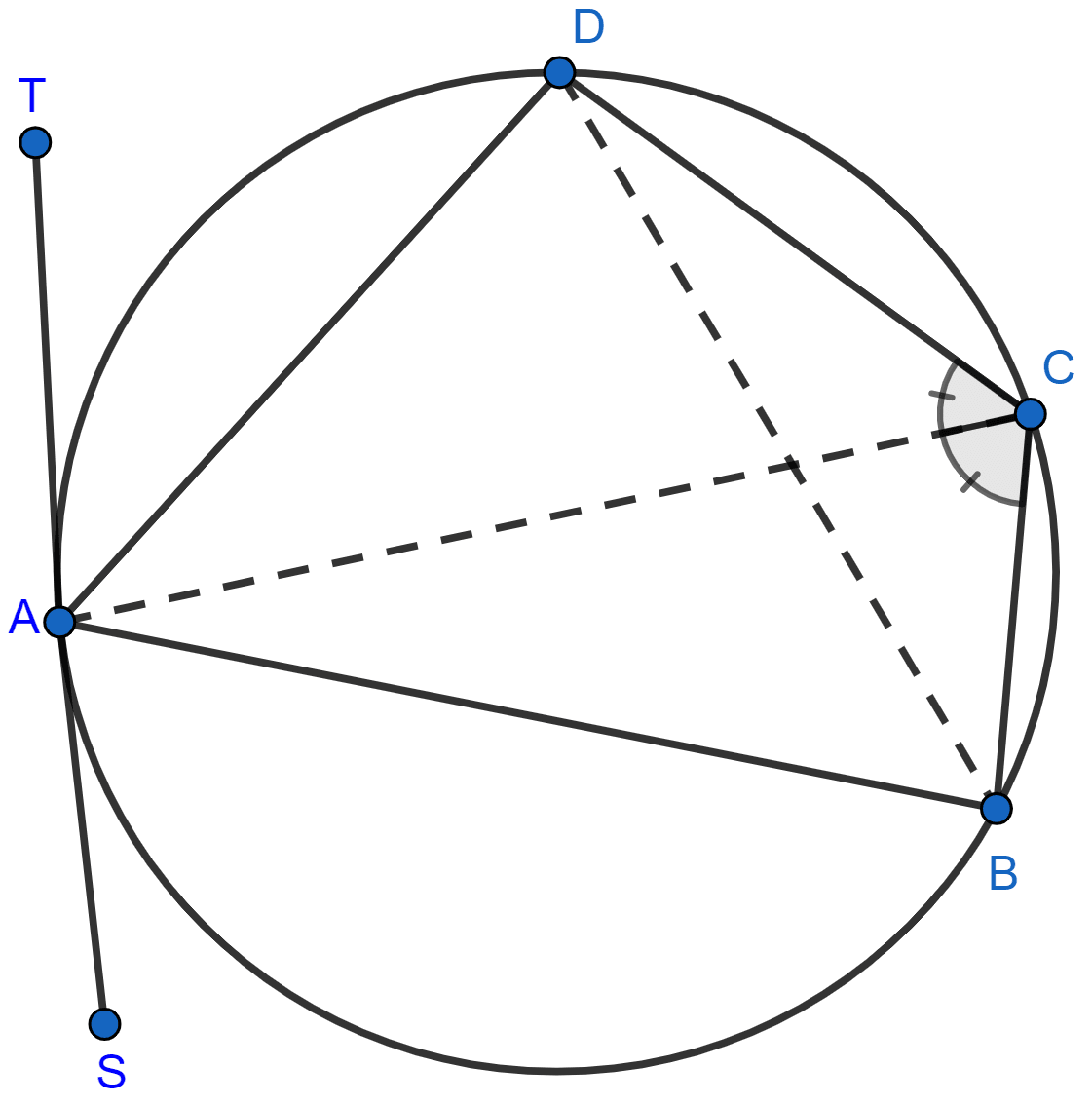
∴ ∠ADB = ∠ACB ………..(1)
Also,
∠ABD = ∠ACD ………..(2)
As, AC bisects the angle BCD,
∠ACB = ∠ACD …………(3)
From (1), (2) and (3) we get :
∠ADB = ∠ABD ………..(4)
As, the angle between a tangent and a chord through the point of contact is equal to the angle in the alternate segment, we have :
From figure,
TAS is a tangent and AB is a chord.
∴ ∠BAS = ∠ADB ………..(5)
From (4) and (5), we get :
⇒ ∠BAS = ∠ABD
Since, ∠BAS and ∠ABD are alternate angles.
Hence, proved that BD is parallel to TS.