KnowledgeBoat Logo

Mathematics

In a △ABC, ∠A = 50°, ∠B = 60°. Arrange the sides of the triangle in ascending order.

Triangles

27 Likes

Answer

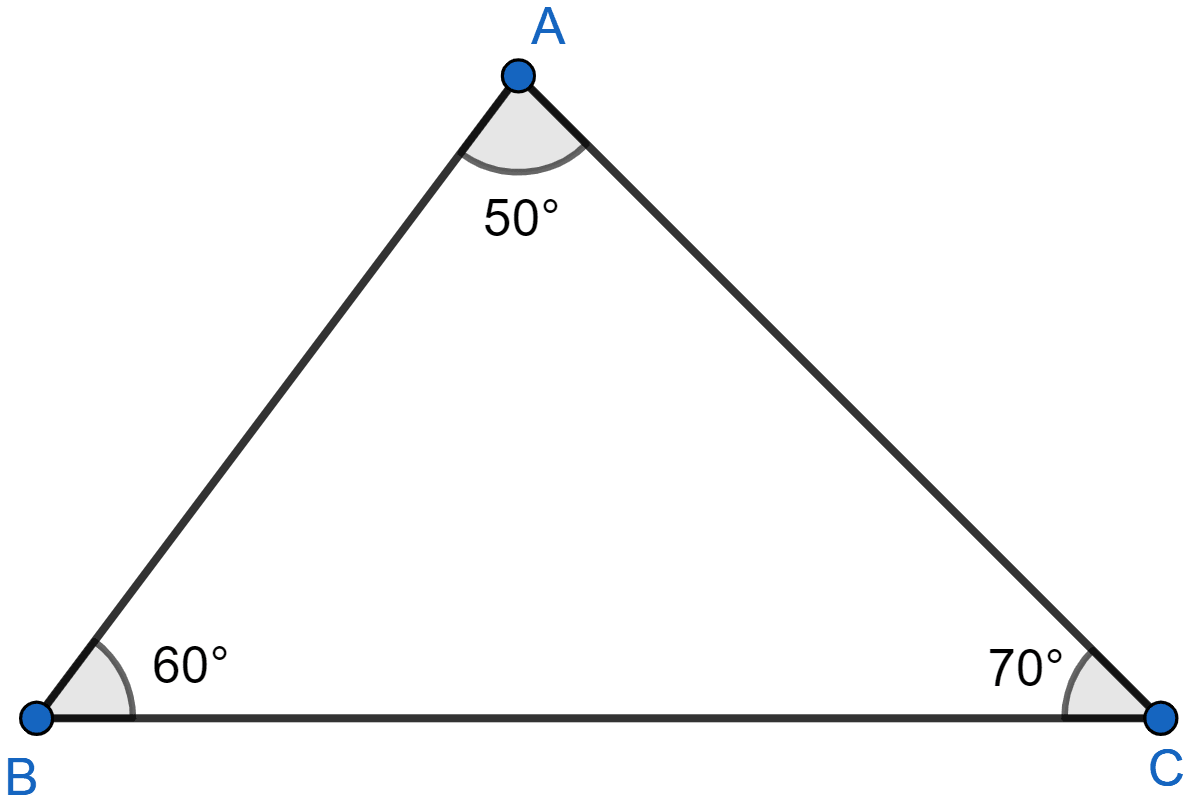
In a △ABC, ∠A = 50°, ∠B = 60°. Arrange the sides of the triangle in ascending order. Triangles, ML Aggarwal Understanding Mathematics Solutions ICSE Class 9.

Sum of angles of triangle = 180°.

⇒ ∠A + ∠B + ∠C = 180°

⇒ 50° + 60° + ∠C = 180°

⇒ 110° + ∠C = 180°

⇒ ∠C = 70°.

So we get,

∠C > ∠B > ∠A.

We know that side opposite to greatest angle is greatest.

∴ AB > CA > BC or BC < CA < AB.

Hence, sides of the triangle in ascending order are BC < CA < AB.

Answered By

21 Likes

Related Questions