Mathematics
If the perimeter of an equilateral triangle is 36 cm, calculate its area and height.
Mensuration
51 Likes
Answer
We know that,
Perimeter of an equilateral triangle = 3 × side.
Substituting the values,
⇒ 36 = 3 × side
⇒ side = = 12 cm.
Area of equilateral triangle =
Substituting the values we get,
From figure,
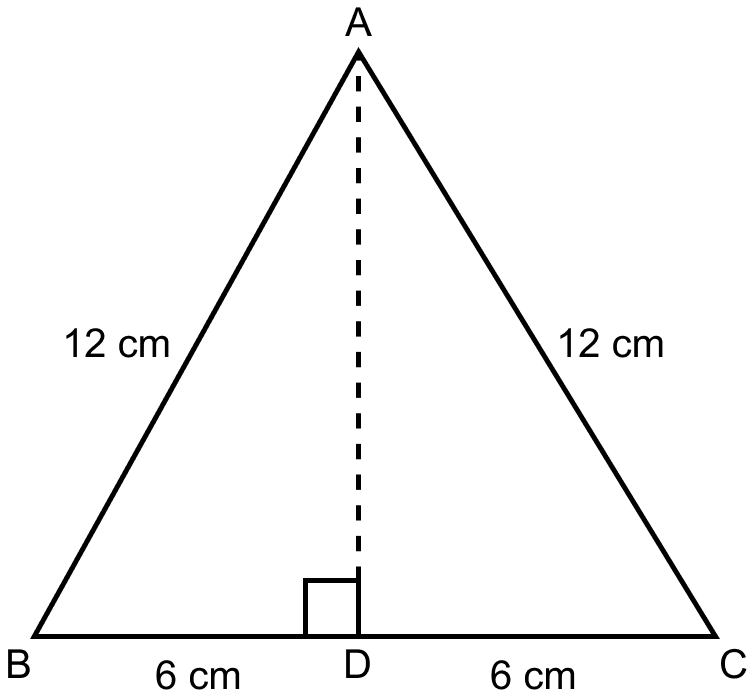
In triangle ABD,
Using Pythagoras Theorem,
AB2 = AD2 + BD2 …….(1)
The perpendicular from a vertex of an equilateral triangle to the opposite side, bisects it.
So, BD = = 6 cm.
Substituting the values in (1) we get,
⇒ 122 = AD2 + 62
⇒ 144 = AD2 + 36
⇒ AD2 = 144 – 36 = 108
⇒ AD = = 10.4 cm.
Hence, area of triangle = 62.4 cm2 and height = 10.4 cm.
Answered By
20 Likes
Related Questions
Find the area of an equilateral triangle whose side is 8 m. Give your answer correct to two decimal places.
If the area of an equilateral triangle is cm2, find its perimeter.
If the lengths of the sides of a triangle are in the ratio 3: 4 : 5 and its perimeter is 48 cm, find its area.
The sides of a triangular plot are in the ratio 3 : 5 : 7 and its perimeter is 300 m. Find its area. Take .