Mathematics
If the perimeter of a rectangular plot is 68 m and length of its diagonal is 26 m, find its area.
Answer
Let ABCD be a rectangular plot of length x m and breadth y m.
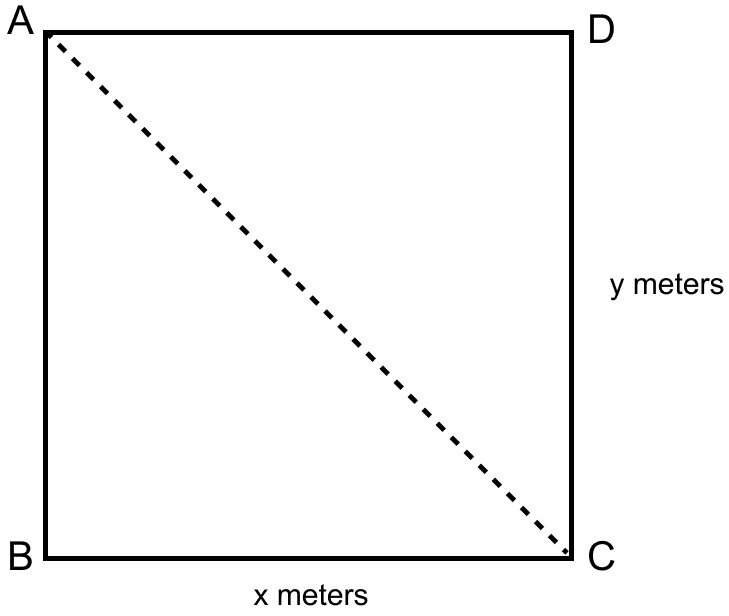
By formula,
Perimeter = 2(length + breadth)
Substituting the values we get,
⇒ 68 = 2(x + y)
⇒ 34 = x + y
⇒ x = 34 - y ……… (1)
In right angle triangle ABC
⇒ AC2 = AB2 + BC2 (By pythagoras theorem)
⇒ 262 = x2 + y2
⇒ x2 + y2 = 676
Substituting the value of x from equation (1),
⇒ (34 – y)2 + y2 = 676
⇒ 1156 + y2 – 68y + y2 = 676
⇒ 2y2 – 68y + 1156 – 676 = 0
⇒ 2y2 – 68y + 480 = 0
⇒ 2(y2 – 34y + 240) = 0
⇒ y2 – 34y + 240 = 0
⇒ y2 – 24y – 10y + 240 = 0
⇒ y(y – 24) – 10(y – 24) = 0
⇒ (y – 10)(y – 24) = 0
⇒ y – 10 = 0 or y – 24 = 0
⇒ y = 10 m or y = 24 m.
Now substituting the value of y in equation (1)
⇒ y = 10 m, x = 34 – 10 = 24 m
⇒ y = 24 m, x = 34 – 24 = 10 m
Area in both cases = xy
= 24 × 10 or 10 × 24
= 240 m2.
Hence, the area of the rectangular block is 240 m2.
Related Questions
The area of a parallelogram is 98 cm2. If one altitude is half the corresponding base, determine the base and the altitude of the parallelogram.
A rectangle has twice the area of a square. The length of the rectangle is 12 cm greater and the width is 8 cm greater than a side of a square. Find the perimeter of the square.
The perimeter of a square is 48 cm. The area of a rectangle is 4 cm2 less than the area of the square. If the length of the rectangle is 4 cm greater than its breadth, find the perimeter of the rectangle.
The length of a rectangular garden is 12 m more than its breadth. The numerical value of its area is equal to 4 times the numerical value of its perimeter. Find the dimensions of the garden.