Mathematics
If the coordinates of the vertex A of a square ABCD are (3, -2) and the equation of diagonal BD is 3x - 7y + 6 = 0, find the equation of the diagonal AC. Also find the coordinates of the centre of the square.
Straight Line Eq
Answer
Diagonals AC and BD of the square ABCD bisect each other at right angle at O.
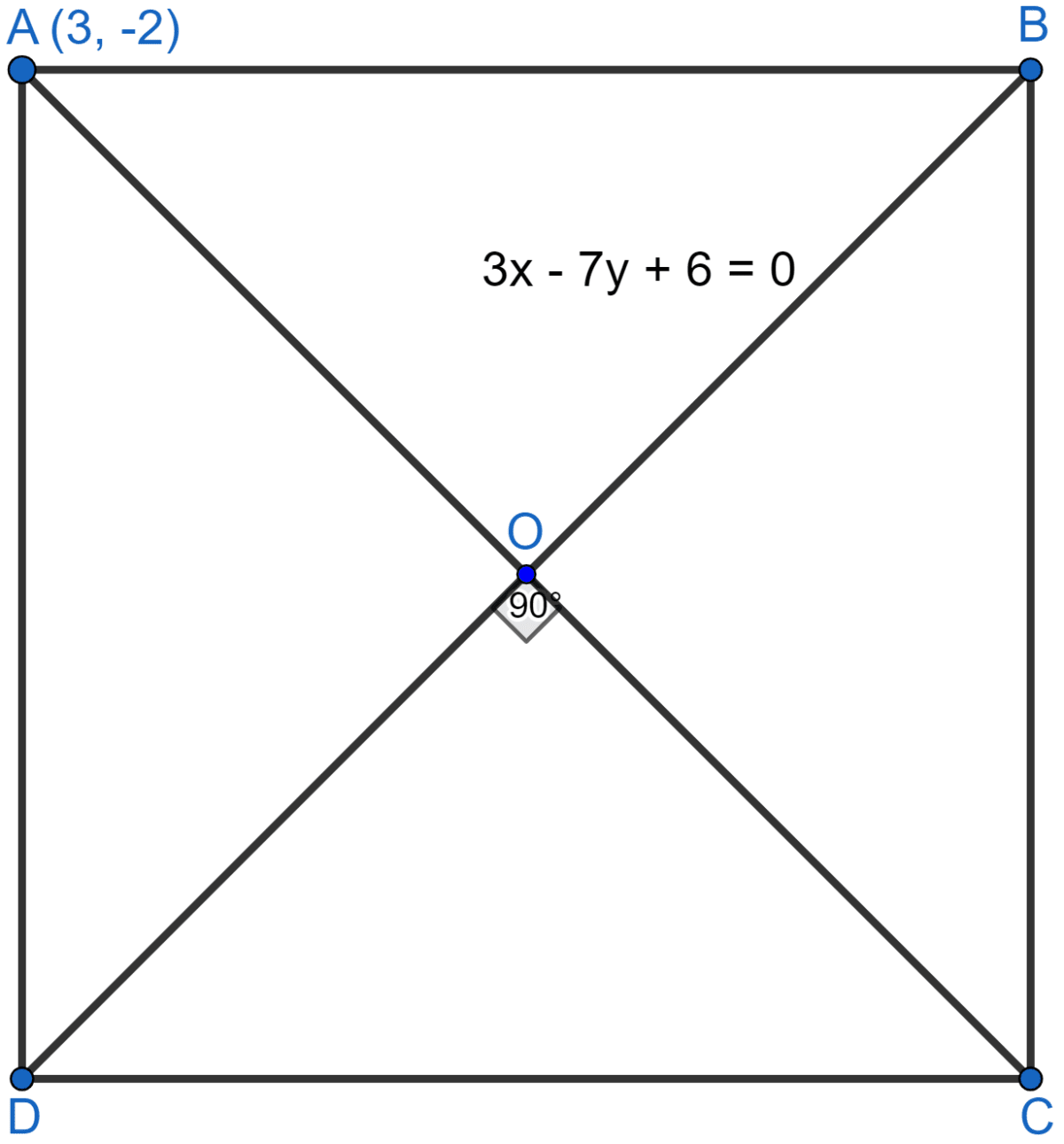
∴ O is the mid-point of AC and BD.
Equation of BD is 3x - 7y + 6 = 0
⇒ 7y = 3x + 6
⇒ y = .
∴ Slope of BD = m1 =
Let slope of AC be m2. Since, BD and AC are perpendicular,
1 \times m2 = -1 \\[1em] \Rightarrow \dfrac{3}{7}m2 = -1 \\[1em] \Rightarrow m2 = -\dfrac{7}{3}.
Equation of AC will be
1 = m(x - x1) \\[1em] \Rightarrow y - (-2) = -\dfrac{7}{3}(x - 3) \\[1em] \Rightarrow 3(y + 2) = -7(x - 3) \\[1em] \Rightarrow 3y + 6 = -7x + 21 \\[1em] \Rightarrow 7x + 3y = 15
Now we will find the coordinates of O, the points of intersection of AC and BD
⇒ 3x - 7y = -6 ….(i)
⇒ 7x + 3y = 15 ….(ii)
Multiplying (i) by 3 and (ii) by 7, we get,
⇒ 9x - 21y = -18 ….(iii)
⇒ 49x + 21y = 105 …(iv)
Adding (iii) and (iv) we get,
⇒ 9x + 49x - 21y + 21y = -18 + 105
⇒ 58x = 87
⇒ x =
Putting value of x in (i) we get,
Hence, the equation of AC is 7x + 3y - 15 = 0 and coordinates of the center are .
Answered By
Related Questions
Find the equation of the line perpendicular to the line joining the points A(1, 2) and B(6, 7) and passing through the point which divides the line segment AB in the ratio 3 : 2.
The points A(7, 3) and C(0, -4) are two opposite vertices of a rhombus ABCD. Find the equation of the diagonal BD.
A straight line passes through P(2, 1) and cuts the axes in points A, B. If BP : PA = 3 : 1.

Find :
(i) the coordinates of A and B.
(ii) the equation of the line AB.
A straight line makes on the coordinate axes positive intercepts whose sum is 7. If the line passes through the point (-3, 8), find its equation.